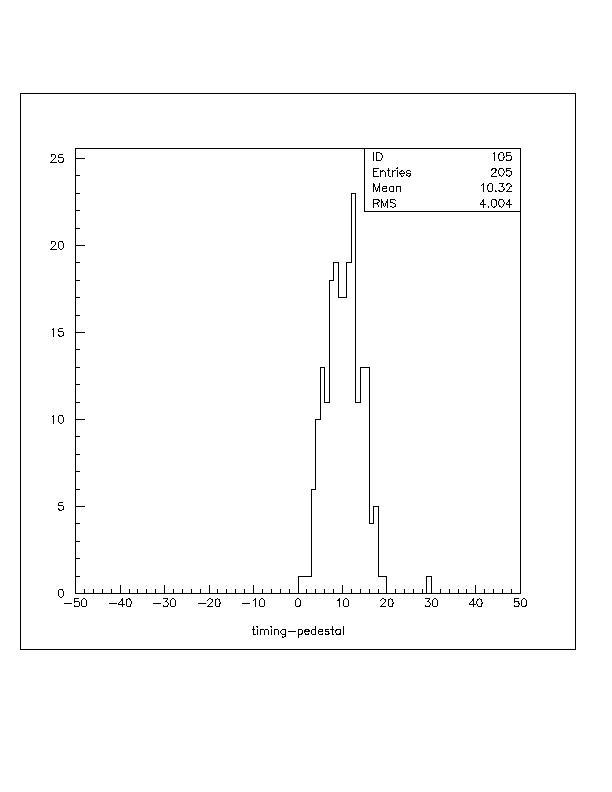
 (Fig.3 Pedestal distributions)
(Fig.3 Pedestal distributions)TIME PEDESTALS
Lazar Fleysher, Roman Fleysher, and Peter Nemethy, with Isabel Leonor.
July 3, 1997
Goal:To find time pedestals of PMT's. Knowing the positions of the laser balls and the travel times of light in water, pedestals can be found.
Motivation
To correctly restore shower front and its direction, one should subtract time-pedestals for all photo- tubes. Ideologically, it means that all PMT's clocks ( TDCs ) have to be synchronized (all time-pedestals have to be found). To solve this problem we used auxilary sources of light (laser balls).
Before the time-pedestals can be determined the speed of light in water and coordinates of light source have to be found (or be given). Only nominal coordinates of the laser balls are known, because the anchor strings are loose for the present water depth, allowing the movement of the laserball rafts inside a circle of estimated radius up to 1.6m. Only a typical index of refraction of water is found in tables, but for our short pulses in a dispersive medium (water) care should be taken to use the group velocity of light. This note describes a method how all these problems can be resolved if positions of all PMTs are known from the survey and all TDCs operate with the same conversion ( in our case 2 counts/nsec). Since the method relays on laser calibration data of varying amplitude, the data has to be slewing-corrected and be taken in a short period of time (to avoid possible "swimming" by the light sources).
Method
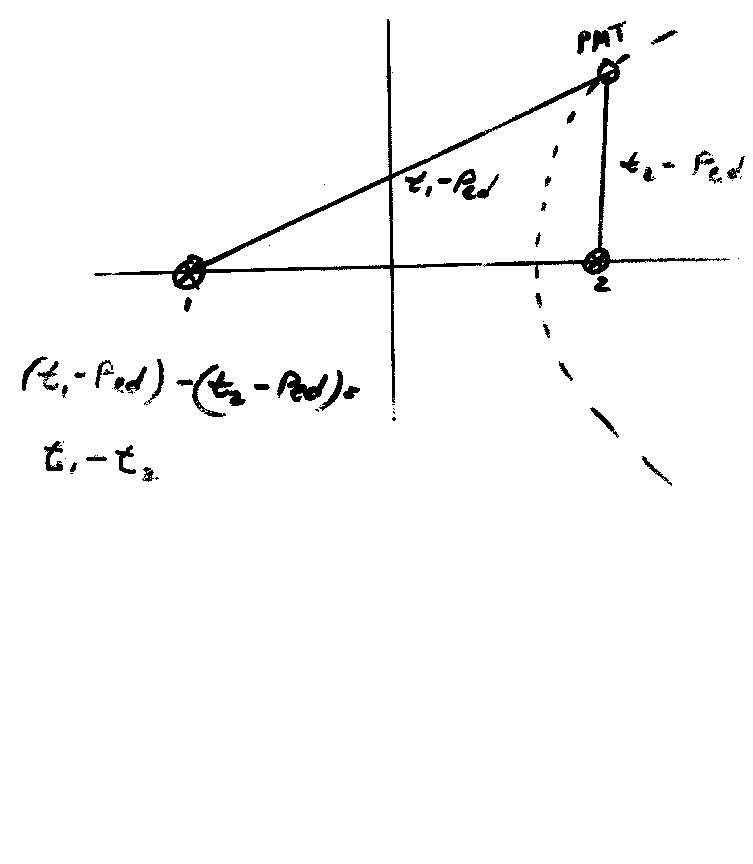 (Fig. 1. The hyperbola of time differences.)
(Fig. 1. The hyperbola of time differences.)
It is not possible to find the position of a single laser ball, considered by itself, prior to knowing the value of the pedestals. However, the positions of a pair laserballs at a time can be obtained by looking at time differences of the two balls, as measured by the same PMT. We define
Tau=T(Ball1 -> PMT) - T(Ball2 -> PMT)
Tau - does not depend on PMT's pedestal!Four different PMT's with their corresponding Tau's for the same laser ball pair would define positions of the foci provided coordinates of PMT's are known. On practice, we used 20 PMT's for an overconstrained fit of ball positions.
In the previous section it was assumed that all the laser balls emit light at the same moment of time. This might not be the case because the propagation time in the fiber might differ from one laser ball to another. Thus, one more free parameter per laser ball pair is required to describe the problem.
The speed of light in water can be either measured or calculated.
Calculation of speed of light in water for green light. Empirical formula for the index of refraction (W. Dorsey, Properties of ordinary water substances, Mafmer Publishing Co., New York, 1968; reference was suggested by Todd Haines) is given by:
N^2(L)=1.76253-0.0133998*L^2+0.00630957/(L^2-0.0158806)where L is wavelength of light in micrometers.
The group velocity of light Vg is given by (Jackson):
Vg/C=1/(N(L)-L*dN/dL)For the green light of our laser:
L=500 (nm) N=1.33646 Vg/C=1.360502 Vg=22.036 (cm/nsec)If we want to measure the speed of light instead of using the above number, one more free parameter has to be introduced in the description, making the total number of parameters equal to six.
4. CALCULATIONS
Within each pair of laser balls the following free parameters are to be determined:
1,2. (dX,dY) - deviations of the Ball1 from its nominal position
3,4. (dX,dY) - deviations of the Ball2 from its nominal position
5. - time delay difference in fiber optics
6. - speed of light in water (if we choose to measure,
not calculate it)
For a given value of the parameters, the predicted value of the time
difference for each of the 20 PMT's is calculated, to be compared
with the experimental time differences obtained from the slewing
corrected timing peaks. The chi-squared of the 20 experimental vs
predicted values is minimized with a matrix-inversion routine by John
Sculli; the minimum yields our fitted values of the parameters.
5. RESULTS OF LASER BALLS COORDINATES SEARCH
For the 5 "good" laserballs we determine the positions using a total of 6 pairs, giving us either two or three independent determinations of a given laser-ball's coordinate.
With the Speed of light set to 22.04cm/nsec and held constant, we find the laserball positions, with fitting errors, given in the table below.
Ball# Ball Pair dX,cm dY,cm ~dR,cm 0 0 - 5 42.6+/-6.0 38.7+/-6.7 57.3 0 - 2 43.2+/-5.6 34.9+/-5.0 55.6 <dX>=42.8 <dY>=36.8 5 0 - 5 8.5+/-6.1 57.7+/-6.3 58.3 5 - 7 11.6+/-5.0 62.7+/-6.8 63.8 <dX>=10.1 <dY>=60.2 7 5 - 7 -46.0+/-4.6 -73.7+/-5.6 86.9 7 - 9 -45.9+/-6.0 -65.8+/-5.7 80.3 2 - 7 -51.2+/-5.9 -68.6+/-6.8 85.6 <dX>=-47.7 <dY>=-69.1 9 7 - 9 -44.2+/-6.1 -45.9+/-6.7 63.8 9 - 2 -60.2+/-5.7 -42.8+/-8.4 73.9 <dX>=-52.2 <dY>=-44.4 2 2 - 7 -220.6+/-4.6 -10.2+/-7.3 220.8 0 - 2 -225.2+/-5.3 -14.6+/-4.6 225.6 9 - 2 -226.2+/-5.3 -15.4+/-5.5 226.7 <dX>=-224.0 <dY>=-13.4
The fitting errors on the positions are typically between 5 and 10cm; the multiple determination of the position of a given laserball is in good agreement for these errors. Figure 2 is a graphic depiction of the deviation of laser ball positions from the nominal. Four of the 5 laserballs are less than 90cm from their nominal position, well within the radius allowed by their leashes. The surprise is laserball 2, at a distance of 2.24m from the nominal, inconsistent with it's leash and nominal position.
We did a very rough check of the laserball positions with Scott D.'s help, by walking on the cover, finding thee laserball rafts "by feel" through the cover, and interpolating from the grid at the edge of the pond. These rough locations (done 4 days after the data were taken, with possible swimming of the rafts in between) are shown as squares on the Figure. The agreement is not overwhelming, but the strange position of ball 2 is certainly confirmed.
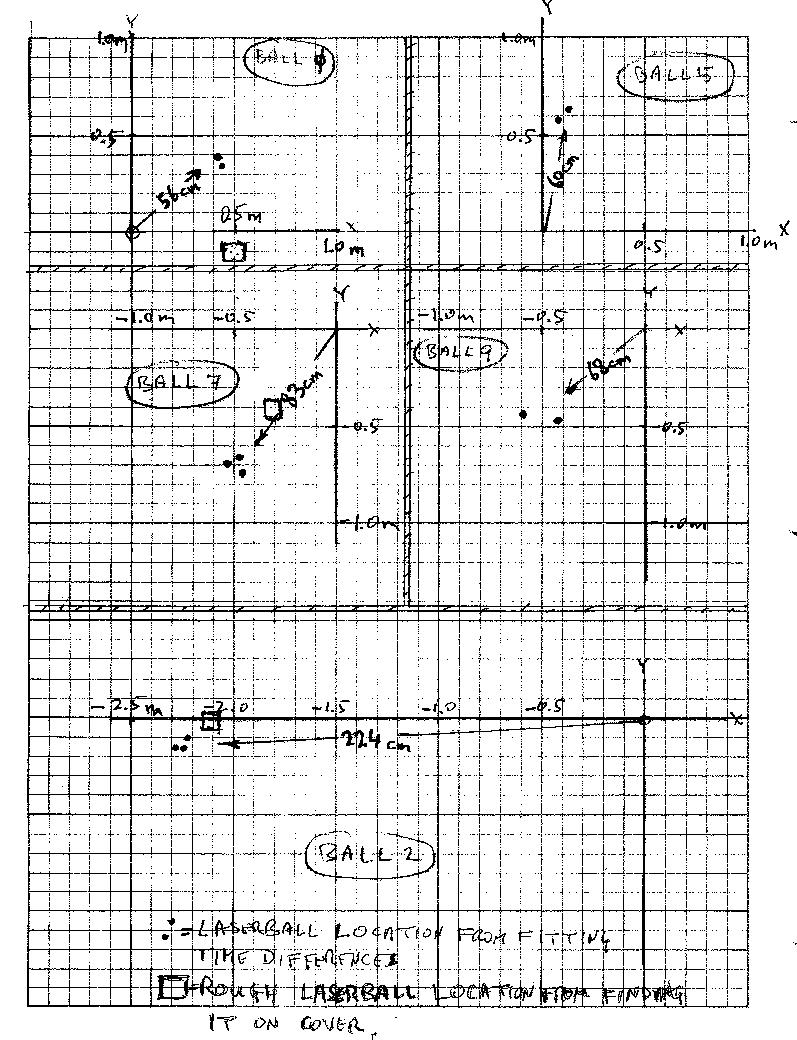 (Fig.2: coordinates of 5 laserballs from their nominal positions.)
(Fig.2: coordinates of 5 laserballs from their nominal positions.)
6. FIBER DELAY DIFFERENCES
From our fit to the data we were also able to find differences in fiber times for different laser balls. These differences should be taken into account when calculating the pedestals. To make appropriate corrections one has to add these times to start times measured from corresponding laser balls. Minus sign says that the fiber is shorter then the reference one (laser ball 0).
Laser ball Fiber delay (counts)
0 0 (definition)
2 -0.2+/-0.5
5 -0.6+/-0.4
7 -0.5+/-0.5
9 -1.6+/-0.6
By allowing speed of light in water vary as a free parameter in our fit, we found it and it is very close to the theoretically predicted value of 22.04cm/nsec (see Section 3, above). The data is self-consistent. The speed was found six times from six laser ball pairs and the results are:
21.92+/-0.6 cm/nsec 21.86+/-0.1 cm/nsec 21.90+/-0.1 cm/nsec 22.02+/-0.4 cm/nsec 21.94+/-0.5 cm/nsec 21.98+/-0.1 cm/nsec <speed>=21.94 cm/nsec
Since position of each laser ball is found from different pairs and positions are consistent with each other, the average of coordinates found are used to determine the pedestals.
The data used for locating the balls and determining the pedestals was taken on June 19, 1997 in a short period of time (about 1 and 1/2 hour) in order to avoid possible motion of the balls during data-taking. Slewing corrected start times were histogrammed, then the peak was fitted. The sigma of the distributions was less then 2 counts in all cases that we used.
To find the time pedestals, we have taken the fitted peaks in the start time and "subtracted" the propagation time of the light from laserball to PMT in the water, by the formula:
PED=PEAK(tstart) + t(propagation),where the strange plus sign is an artifact of our "common stop" mode, which means that tstart is in backward time, while t(propagation) is in forward time.
The file PEDS_FIBFIX.DAT contains the pedestals for 205 PMT's calculated with the assumption of identical fiber-light-guide propagation times, with Fig.3 showing the distribution of the pedestals. The file PEDS_FIBDEL.DAT contains the pedestals adjusted by the observed relative fiber propagation times, a maximum change of 1.6 counts in pedestal values.
 (Fig.3 Pedestal distributions)
(Fig.3 Pedestal distributions)