This note describes some ideas I have on a method to a priori select "good" PMT hits for use in the initial shower plane fits. Further analysis is required to refine this idea for use in the Milagro reconstruction code(s). Comments and questions are especially encouraged.

Introduction

A general difficulty in performing reconstruction of data such as that from Milagro is initially deciding which PMT hits should be used in the reconstruciton/fitting procedures. The performance of any subsequent fits is always very dependent on this initial selection. As an example, for Milagro plane fits, an out-of-time PMT can strongly influence (~1 degree or more) the fit direction, potentially resulting in a selection of a biased (by the out-of-time PMT) set of PMTs to use in subsequent (e.g. using tighter cuts on fit residuals) fits. This may be especially true of large pulseheight hits that are caused by a nearby, late muon--normally one would think large pulseheight means that it is a good hit, likely near the core and therefore in time, but large pulseheight may also mean a particle passing nearby.

The idea here is to try to eliminate out-of-time PMTs from use in any fitting in an unbiased way; here unbiased is meant to mean no bias with respect to knowlege of the shower plane direction. I am not trying at this point to make very tight cuts to eliminate slightly out-of-time PMTs (actually, they should be used in the fit and receive appropriate weight in the likelihood or chi-squared), but eliminate those that are obviously bad.

The idea is to take advantage of the fact that we know that hits due to the shower plane (e.g. not noise hits, not late muons, etc.) must be causally related. In our case, this means that the hits should be separated in time by no more than they are separated in distance, using the known propigation speed of the plane; they can be separated in time by less than in distance, but not by more. Because we are dealing with both the speed of light, and the speed of light in water, I will make the conservative choice of the slower speed here. Each PMT hit will be tested to determine if it is causally related to the event.

Some Method to the Madness

One must choose how to implement the causality requirement in practice. To simplify matters, I have chosen to only look at times/distances between nearest neighboring PMT hits, where nearest includes the 4 PMTs 1 lattice spacing away from the candidate PMT, and the other 4 at sqrt(2) times further away, for a maximum of 8 potential neighbors. I use only those hits labled "good" by the on-line edge finder, and use the on-line calibration of times and pulseheights; Tony has some worry about the on-line slewing calibration below 1 pe. To be sure all PMTs are the same, I ignore the PMTs on the outside edges that have at most only a maximum of 5 neighbors. The data sample used for this study is the first 10,000 events from run 211, subrun 75 sitting on disk here in Los Alamos.

Since I do not know a priori the direction of the shower, I do not know the sign of the causally related time difference i.e. if my candidate PMT should be earlier or later than its neighbor. I do know however that the absolute value of the time difference between neighbors ought to be less than the distance between them divided by the speed of light in water, that is the maximum expected time-of-flight (ToF) between the two PMTs. Again, to simplify matters, I take the maximum ToF to be that between the candidate PMT and its furthest neighbor, or 17.5 ns (= 9.3' * 1.414/(1'/ns / 1.33)). So, in what appears below, T-ToF will be the absolute value of the time difference minus the 17.5 ns above.

A Cursory Look at Some Results

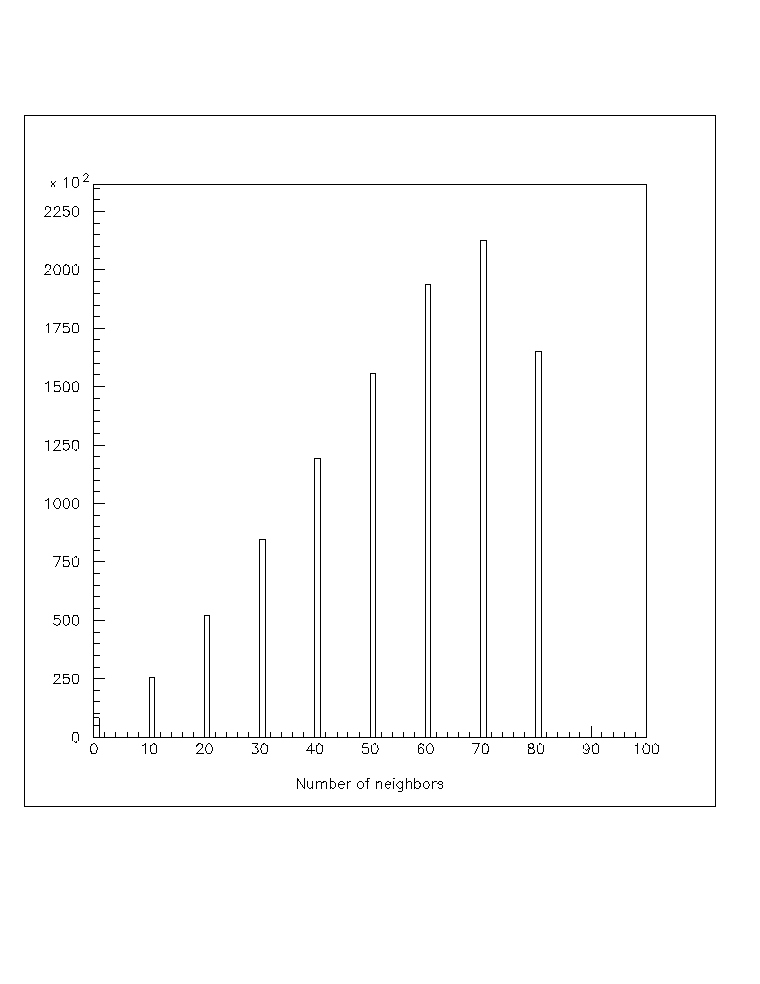
A first look at some results in quite interesting. You will have to download or view the .ps files to see these figures in detail--sorry for the pain but the ps to gif conversion really trashes the figure. Shown below is the distribution of the number of neighbors that each PMT has

Fig 1.: The distribution of (10 times) the number of neighbors for each PMT; the average number is about 5.5 neighbors. Download plot1.ps for a better view.

It is very rare that a PMT has only 1 neighbor; about 1% of our hits are in PMTs with no neighbors. This is due at least in part to our rather high threshold of 100 PMTs for the trigger, but frankly is much lower than I would have expected.

Next it is interesting to see the time difference (w/o ToF subtraction) between neighbors as a function of pulse height. This is shown here:

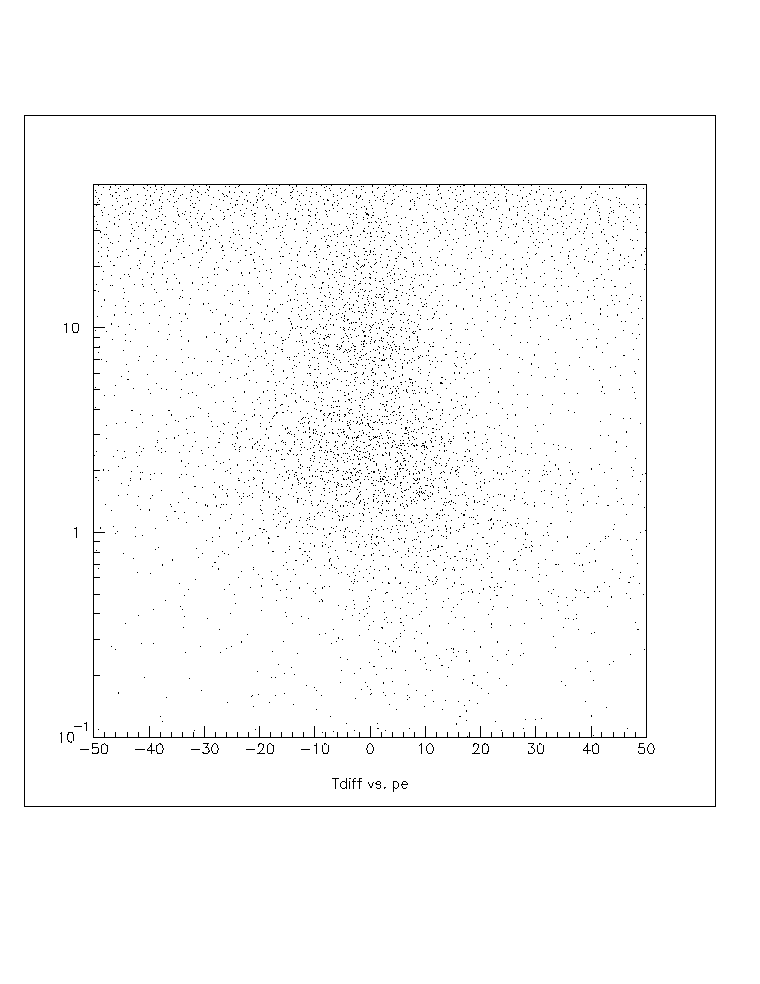
Fig. 2: The log of the pulseheight (in pe's) for the candidate PMT vs. the time difference (ns) wrt. its nearest neighbors. Again, download plot2.ps for a better view.

You can see from the plot what looks like a slight correlation of the time difference between the candidate PMT and its neighbors and the PMT's pulseheight. It appears that the candidate PMT is hit earlierer than its neighbor at high pulseheights (though I will admit that the correlation may not be real--don't beat me up on this one, ok?). If true, this is perhaps most likely due to the quality of the on-line calibration to account for slewing, though it may be a physical effect due to, for example, prompt muons punching down near the PMT and causing an early hit, or perhaps prepulsing, or something else. It should not be what is often called a "sampling" correction as the two PMTs are at nearly the same place in the shower plane.

As a sanity check, the next figure shows the number of neighbors that a PMT has compared with its pulseheight. One would expect that, for the most part, large pulseheight hits would have lots of neighbors as the large pulseheight PMT is in a dense part of the shower.

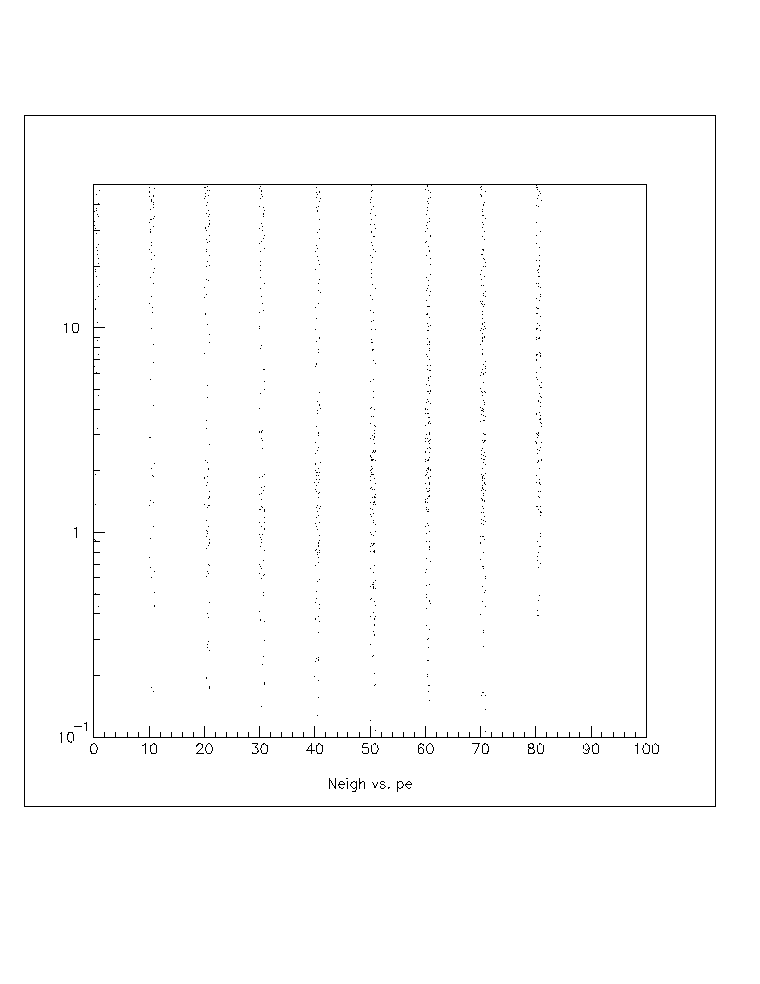
Fig. 3: Showing the relationship between the pulseheight of a PMT and (10 times) the number if neighbors. Download plot3.ps for a better view.

At least I am not completely insane--there is some positive correlation between the pulseheight and number of neighbors. I hope you can see another interesting feature--that is for hits with 0 or 1 neighbor, the pulseheight tends to be rather high. I expect this is again due to single, isolated particles (likely muons) in the event passing near a PMT.

The next plot shows the T - ToF difference between each PMT and its neighbors. Just to remind you, the hits at positive T - ToF I would consider acausal--they are not related to the main shower plane.

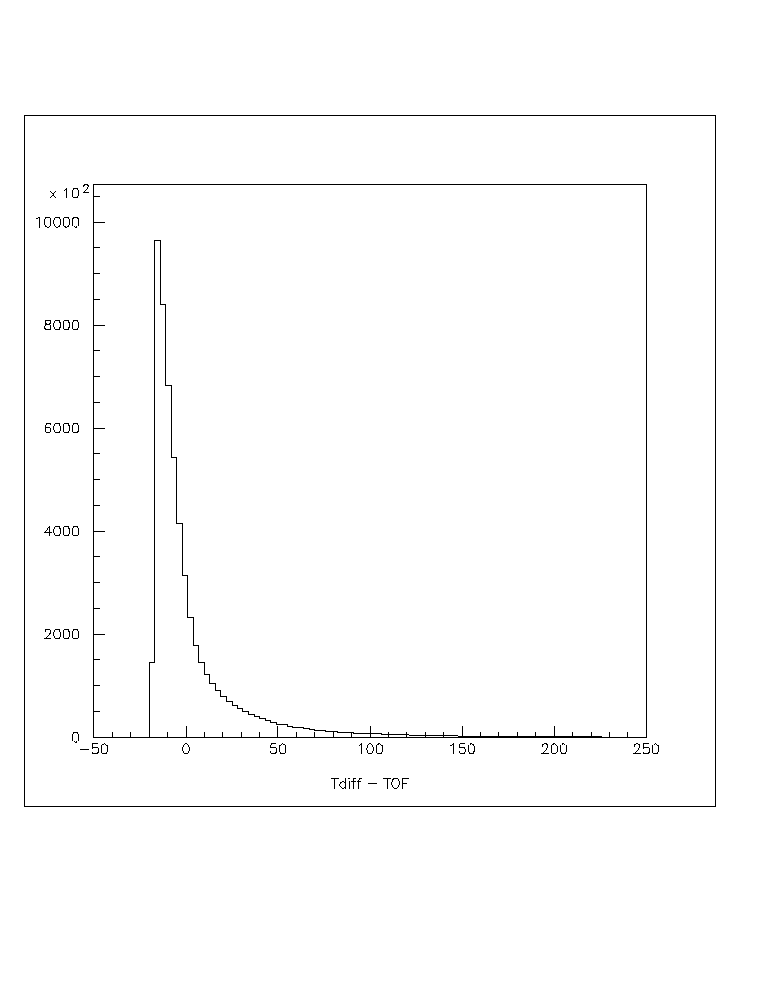
Fig. 4: The time - time-of-flight distribution for all PMTs with at least 1 neighbor. Check out plot4.ps to see the figure in detail.

This distribution does not show any clear break that would distinguish good hits from late hits, as one might have expected. This distribution however shows the power of the proposed cut. For large time differences (say those later than 10 or 20 ns) between neighbors, it is clear that at least one of the hits is not at all related to the main shower. As stated before, I have yet to formulate a proposed cut based on these results--that is the next step.

Again as a further sanity check, the next three plots show the same T - ToF distribution, this time selected by the number of neighbors for the candidate PMT. One would expect that hits far out on the edges of the shower, where the density, and therefore number of neighbors, is low, to be most often due to late particles.

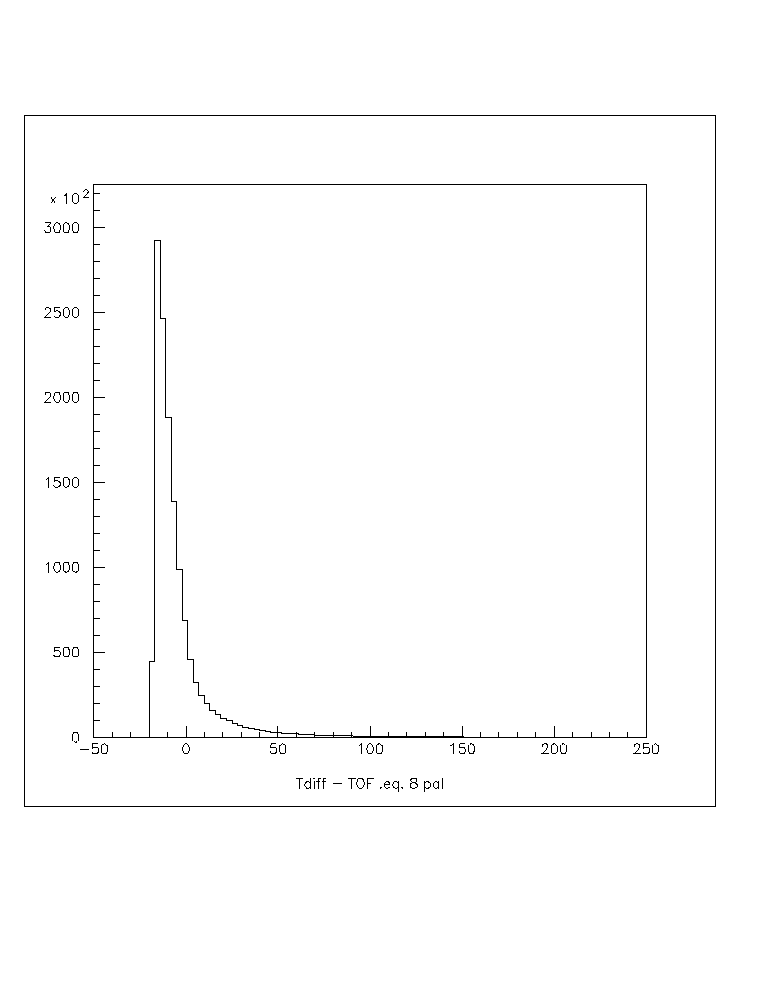
Fig. 5a: T - ToF for those hits with 8 neighbors. plot7.ps to print/view.

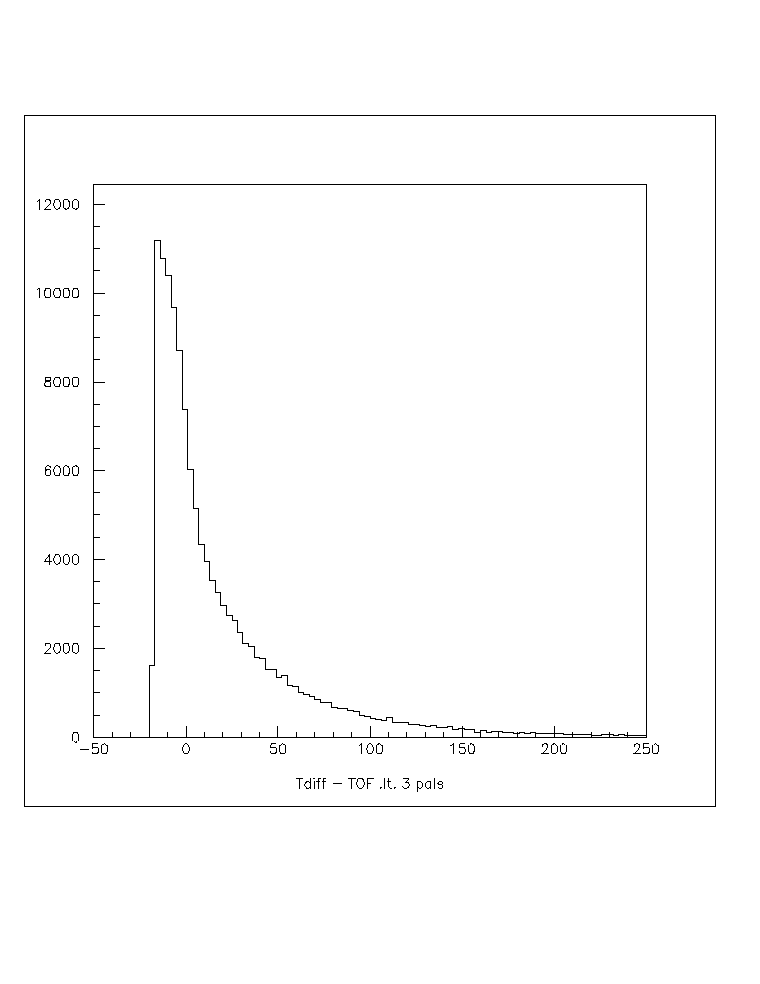
Fig. 5b: T - ToF for those hits with 1 or 2 neighbors. plot5.ps to print/view.

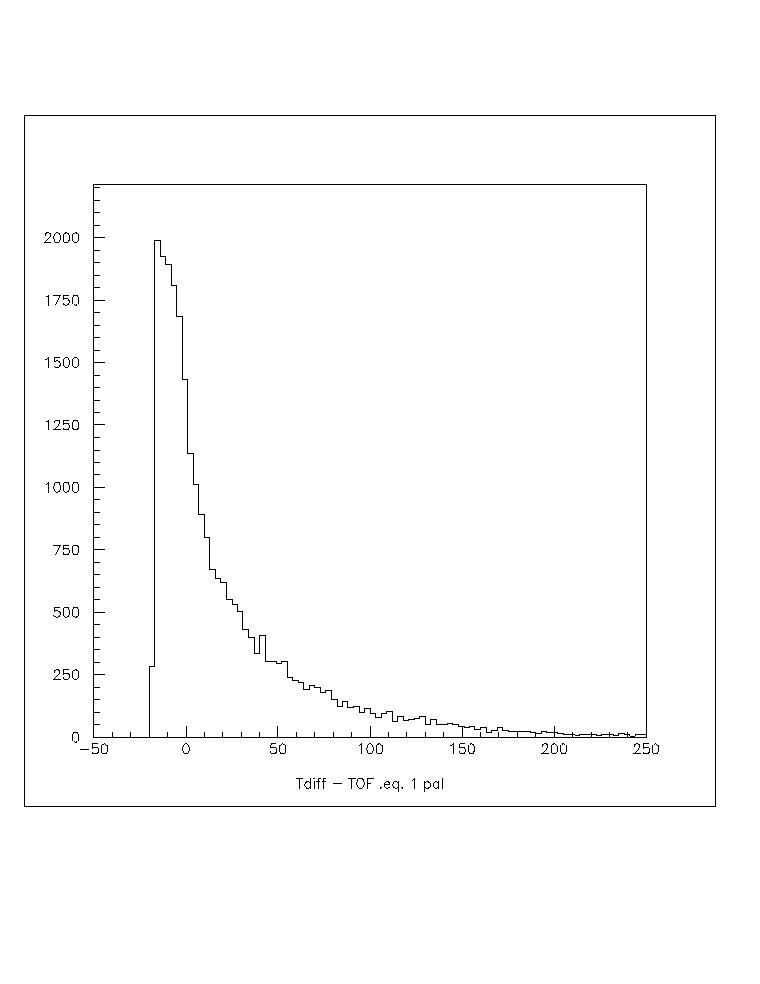
Fig. 5c: T - ToF for those hits with only 1 neighbor. plot6.ps to print/view.

It is clear from these figures that, as expected, the hits in the sparser parts of the shower tend to be more likely from late particles. A brief summary of this is given in the following table:

# Neighbors ----------Fraction w/T - ToF < 0
-------------------------------------
All ------------------- 69%
8 -------------------- 82%
< 3 ------------------- 46%
1 ---------------------43%

Summary

I find these results encourage further investigation in using a causality criterion as an unbiased, a priori selection of PMT hits for shower plane fitting. They clearly show that a large fraction of our hits are poorly related to the air shower plane, consistent with the results of the on- and off-line fitting. The main difference is that the on/off-line fitters require some knowlege of the air-shower direction as they make their timing cuts.

P.S. Thanks to Stefan for helping me get going on this analysis--you can teach old dogs new tricks!