In this Mini-report, I show "work in progress" on understanding
our angular resolution and the stability of our fits. The main
point of this work is to compare two measures of angular resolution
which are somewhat different than deleo. The first is the angle
difference on an event by event basis between Tony's online fit
and my refit of the event using a different fitter. The second is a comparison,
again on an event by event basis, of what happens when you jiggle
the times of each counter and refit it using the same fitter.
Neither are a direct measure of our angular resolution, but both
are related to it.
I took a data file from the online system May 25th - Run 222 subrun
69. All results contained here are from that data.
I wanted to compare our old Cygnus (iterative and weighted) fitter with the online fits using Tony's code (NOTE: they should be very close to the same). I read in the data and convert it using the CalibrateRaw routine. This returns times and pulse heights from the compressed data. I also read in the angle and fit parameters from the online fit.
At this point I fit the data using my fitter which I describe here. I start with the old Cygnus routine skylwgt.f. It is basically unmodified except that it allows various weighting functions to be used. (For those of you who remember, this is the version before we put the refit code into the fit routine so I have to toss counters manually). The weighting functions I choose to test are:
if(wgt_type.eq.1)then
s=sgl(j)
if (S.gt.100) then
sgg = 2.5
else
sgg = 2.5 + 4.0*exp(-0.2*S)
end if
wgt(j) = 1./(sgg*sgg)
endif
if (sgl(j). le. 5) wgt(j) = (sgl(j)-.5)/4.5
else wgt(I)=1.
I first fit the data once using all tubes above a threshold pe
value. This is adjustable. For most of this paper I will present
results with a pe cut of 1.0 (~what Tony used) and his weighting
algorithm.
After the first fit I then start the process of tossing "bad"
tubes. I do this in a way that will minimize the chances that
one really far off time screws up the entire fit. What I do is
find the biggest chi value and throw out counters that are at
least half of that time off the plane. This process is iterated
until the worst counter is no more than 20ns (so we keep guys
10ns or less). I then compute chisquared for this fit and get
the angles.
I find the space angle difference between my fit and Tony's (as
recorded in the data). These will be different even when we use
the same algorithm because Tony uses a different edge finder and
even a slightly different calibration. This is called "delangle".
Another thing I do is shake my fit. What I mean by this is I take
each time that comes from the data and I wiggle it with a gaussian.
For example, when I am using Tony's weighting scheme, he gives
a timing sigma of sgg = 2.5 + 4.0*exp(-0.2*S). I wiggle the timing
of each hit tube by a gaussian with width sgg/2 and is centered
at the actual recorded time. (If I am using the Cygnus weights
I wiggle by a gaussian with 2.5ns width.) After wiggling each
tube in an event, I put the event back into my fitter from the
beginning. I once again toss tubes and refit the event. I then
compute the space angle difference (in degrees) between my original
direction and the wiggled output. This is called delwiggle. In
this document, when I refer to theta or chisquared it always refers
to my original final fit (after tossing counters, but before wiggling).
The point of this study is that del wiggle is a measure of our angular resolution - Note: I am not saying it is our angluar resolution but that it must be a measure of it - factors of root two may well be there!
The key thing is that if you shake things by half of sigma
and the angle changes by say 1 degree, then the angular resolution
can't much better than 1 degree because you don't know the timing
to better than half a sigma anyway. So this gives us a method to
explore our resolution against various parameters with a different
set of baises from deleo.
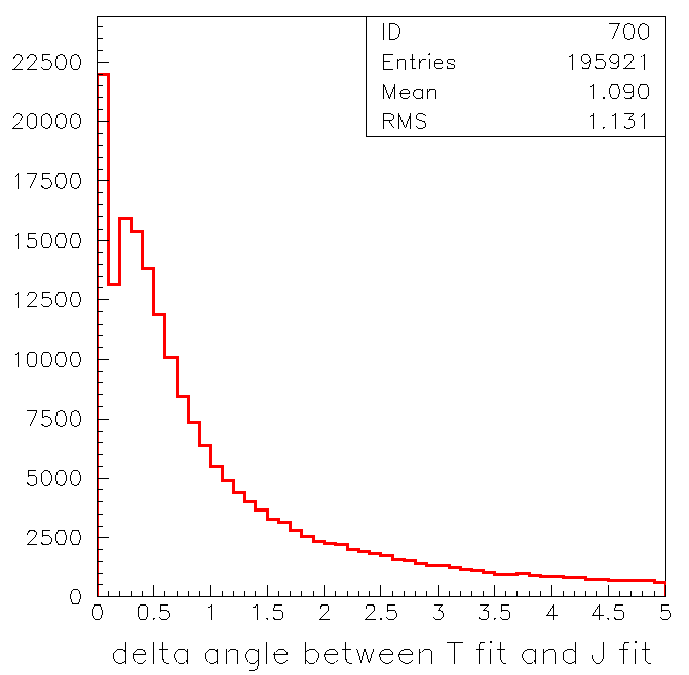
Figure 1 shows the angle difference, delangle between Tony's fit
and mine with no cuts:
Note the average is truncated at delangle of 5 degrees.
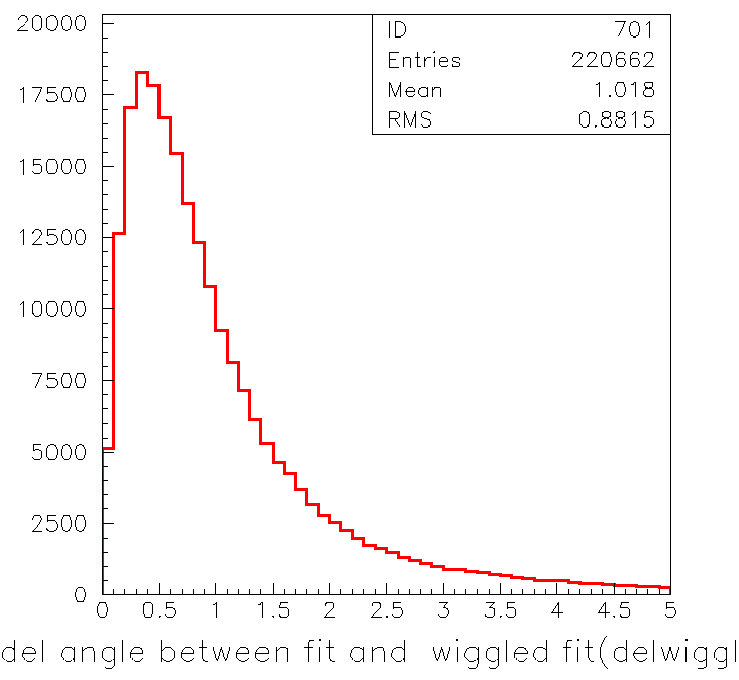
In figure 2 we see the angle difference between the wiggled event
and the original. Note the similarity to delangle.
Now it is reasonable to want to see chisquared so below we plot
chisquared for my fit: 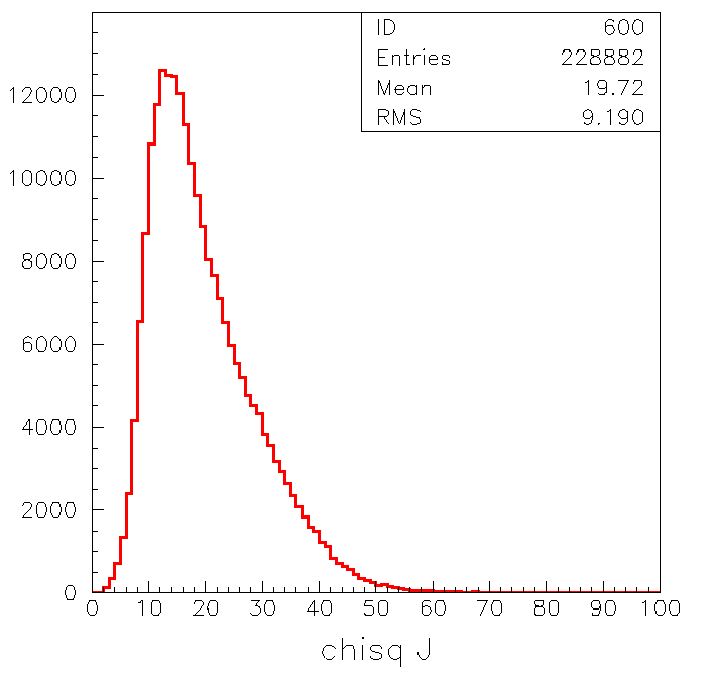
We can now go back and ask what happens to the first plots if we impose a chisquared cut of say 30.
The next figure shows what the delangle and del wiggle look like
with this cut.
Note that these are a little better than before but not much.
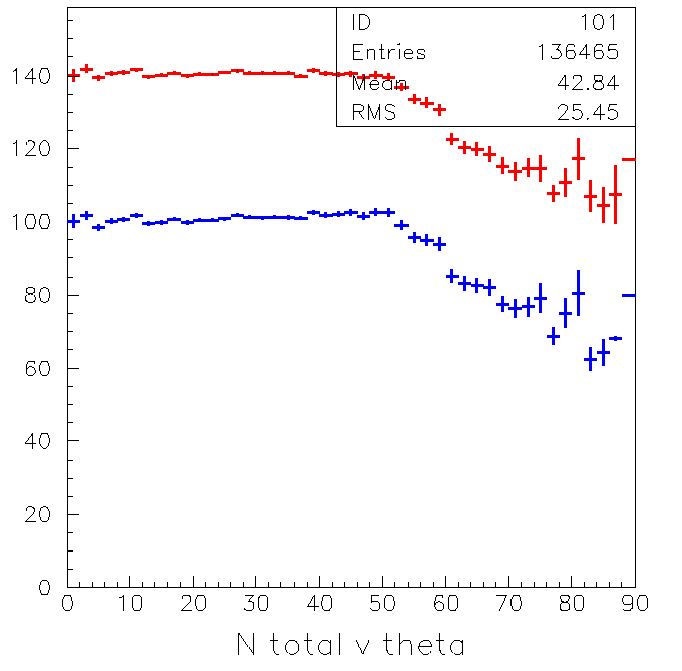
Now we can look at the number of tubes above the 1 pe as a function
of angle:
Note that the average starts to drop above about 50 degrees.
In the next plot we see that the total number of pmts (red) and
the number above 1pe (blue) note that they track perfectly.
The next two plots show how delangle and del wiggle increase with
chisquared.
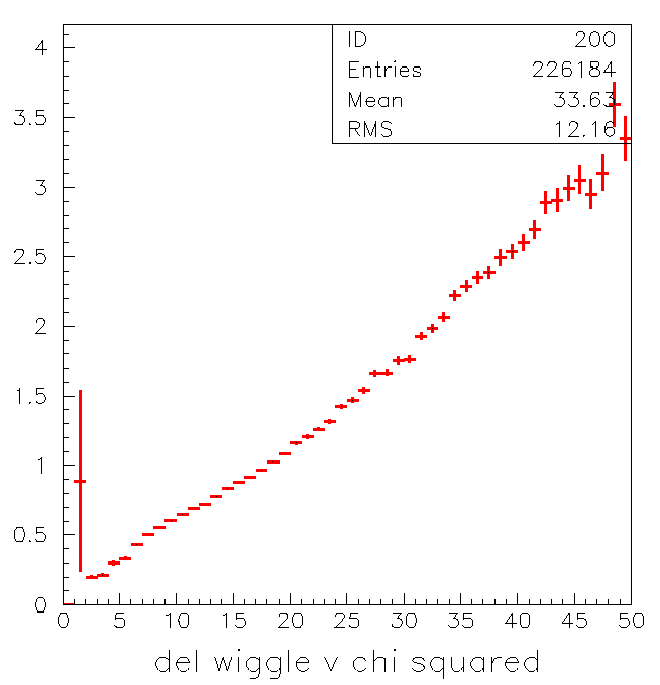
It seems that del wiggle is even more a linear function of chisquared
than delangle. This is probably because its using the same fitter.
Next we look at how chisquared goes with the polar angle of the
event (theta). To make sure we were not looking at very small
showers we put a cut at a minmum of 50 pmts in the fit (after
tossing).
Next we show how both delwiggle (blue) and delangle (red) vary
with angle
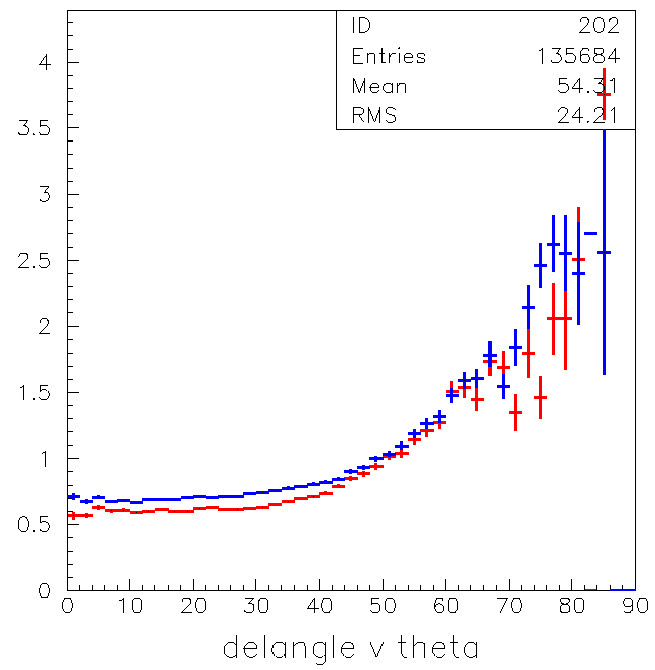
Its clear they both behave the same and show a disturbingly large
increase above about 45 deg.
Well I thought maybe the problem was that the number of tubes
went down with theta so I can check that out.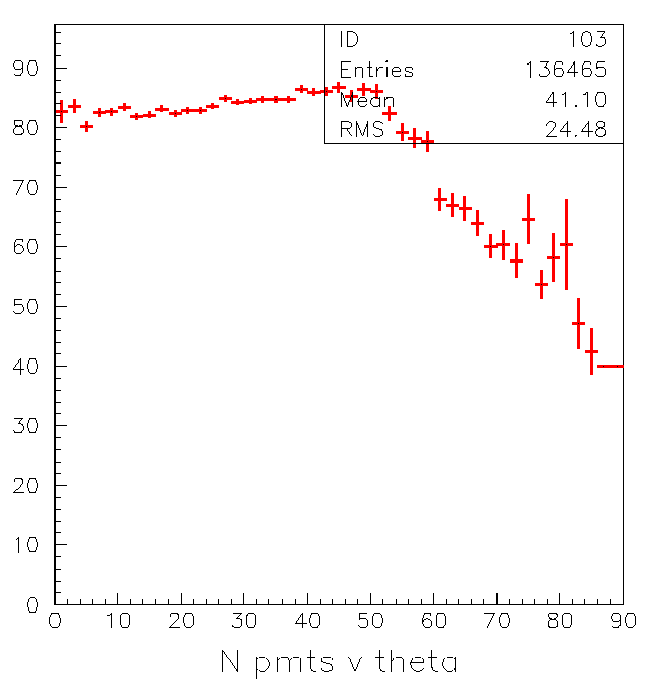
Indeed the number of tubes does drop with theta!
So what about tubes we are throwing out? Well first we can look
at this question of bogus tubes in general.
How does the number of tubes tossed from the fit depend on the
number of tubes above threshold? Take a look: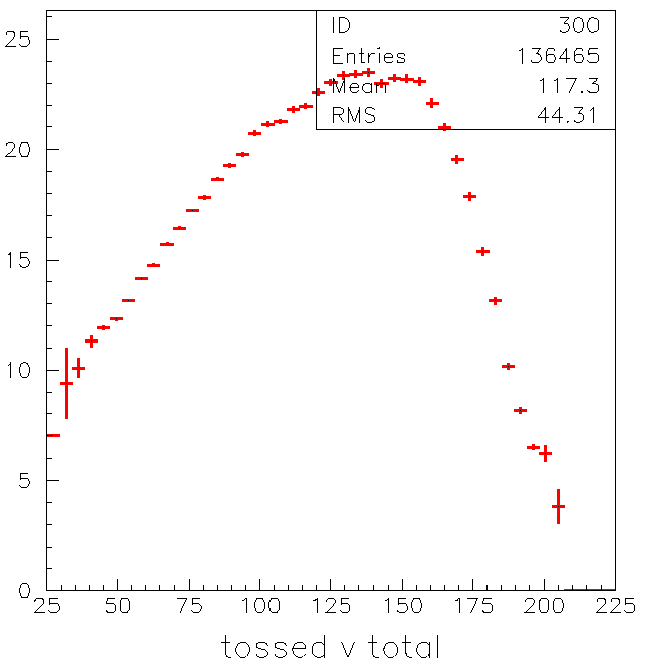
This is an interesting shape. Maybe we can look at it as a fraction:
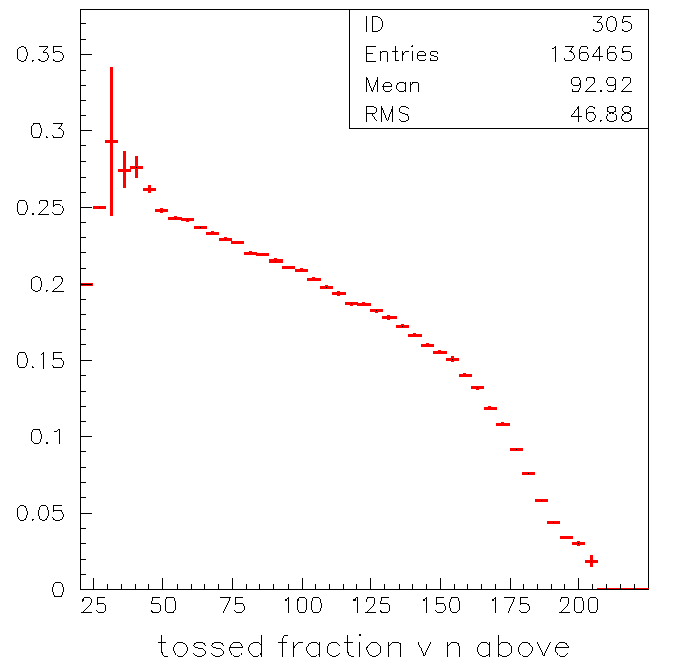
It suggests to me that the number of tubes tossed depends on the
amount of tubes available to be hit by stay light.
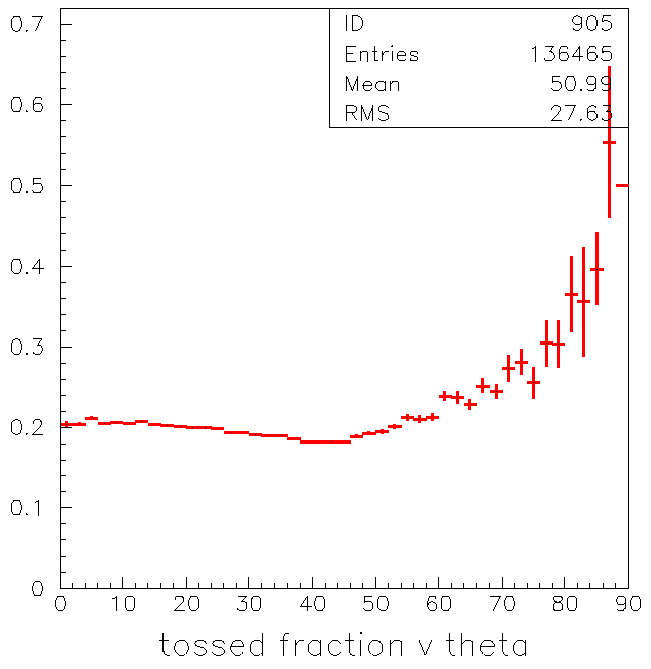
You can see in the plot below that the fraction tossed increases
with angle as well:
So now we can look at how are angle differences vary with the number of pmts used in the fit (npmts). These are the number remaining after the final fit.
Now for del wiggle:
I'd be hard pressed to suggest we use any fits for tubes less
than 50 or maybe higher. So lets see if using 50 or 70 pmts in
the fit make things better at large angles:
Conclusions
So it looks like the resolution gets worse at large angles even if you choose lots of tubes. This looks bad for our moon study. Why? It seems curious to me that the resolution gets worse just when some of the light starts going horizontally or upward (48 degrees). I think this may be why Todd does not see a clear causality break. (See Todd's mini report). Some of this light may be nearly horizontal light that hits tubes from below or bounces off the water surface (via internal reflection). I want to implement Todds nearest neighbor algorithm soon and look at what it does at large angle.
There are many other plots that can be made. These plots
are only for the run using Tony's fitter. The others look similar.
More work needs to be done after the calibration is complete.
You can get the postscript version of this and the other runs in http://umdgrb.umd.edu/~goodman/grito_plots/
jag50.ps is this one
jag51.ps is cygnus weights
jag52.ps is no weights (NOTE THAT DELWIGGLE will be bogus for this one.
Jag53.ps is
the same as jag50 except that the cut is 0.5 pe.
For the exact details of how each plot was made you may want to
look at the profile_w.kumac file in the same directory.