Milagrito Angular Reconstruction
Gus Sinnis
September 3, 1997
In this memo, I explore the utility of the standard CYGNUS angle fitter for Milagrito data. Unlike CYGNUS, the timing distributions in Milagrito have exceptionally long late tails at small pulse heights. Thus, one would expect a fitter that is based on a Guassian model for the timing residuals to perform poorly. The point of this memo is to determine a baseline: how well does the Chi squared method work for our data and is there a subset of the data for which this technique yields acceptable results?
| Sampling Correction |
| Weights as a Function of PEs |
| Fit Results (Deleo, etc.) |
| Fit Results (Deleo, etc.): RELAXED |
| Comparison to Previous Fitter |
| Conclusions |
The Data Set:
For the following analysis I have used the slewing corrections as derived from the laser calibration data by Isabel Leonor, the timing pedestals (also from the laser data) as derived by Peter Nemethy, Roman and Lazar Fleysher, and the TOT to PE conversions derived from the ADC by Kelin Wang.
The problem is then to measure the sampling and curvature corrections from the data itself. To do this one requires an angle fitter. However, without the proper sampling corrections the results may be biased. To minimize such problems the following cuts where made on the events:
A slightly modified version of the online fitter was used in this preliminary pass.
Technique:
After the angle fit is performed the residuals from all of the hit PMTs are calculated and stored in a 2-D histogram: Tchi(PE,Rcore). For PE bin the average Rcore is found and for each Rcore interval the average PE value within the PE bin is found. These true averages are used in deriving the sampling and curvature corrections. The table below gives the results (in ns) of this preliminary pass at the data. As "usual" a negative time corresponds to a late arrival time.
| PEs | Rcore | Median | Peak | Average | RMS | Nentries |
| 0.267095 | 7.118501 | -22.5 | -8.5 | -16.23145 | 14.83136 | 160732 |
| 0.264923 | 15.15495 | -26.5 | -4.5 | -13.98170 | 15.38400 | 437384 |
| 0.296054 | 24.46268 | -25.5 | -7.5 | -12.79270 | 14.94166 | 338626 |
| 0.345033 | 33.91194 | -24.5 | -6.5 | -12.57292 | 14.91664 | 125898 |
| 0.371727 | 42.40936 | -22 | -2.5 | -12.03710 | 14.93752 | 17087 |
| 0.723976 | 6.980463 | -17 | -6.5 | -15.36188 | 13.74021 | 126717 |
| 0.716533 | 15.17315 | -19.5 | -5 | -13.47943 | 14.57037 | 314504 |
| 0.712671 | 24.70510 | -19 | -5.5 | -12.23524 | 14.1936 | 291509 |
| 0.711906 | 34.19790 | -19.5 | -5.5 | -12.21947 | 14.43905 | 156349 |
| 0.720642 | 42.53039 | -19.5 | -7.5 | -11.71681 | 14.57728 | 29292 |
| 1.4653 | 6.817902 | -11 | -4 | -12.88333 | 11.96277 | 154906 |
| 1.454009 | 15.04027 | -11 | -3.5 | -12.12933 | 12.96005 | 316758 |
| 1.450059 | 24.61347 | -10.5 | -4 | -10.96694 | 12.54672 | 258771 |
| 1.444222 | 34.16461 | -10.5 | -4.5 | -10.82554 | 12.72309 | 126540 |
| 1.428921 | 42.48268 | -11 | -2 | -10.55157 | 13.15150 | 22211 |
| 2.477205 | 6.64449 | -7.5 | -4 | -9.740786 | 10.25593 | 110235 |
| 2.469505 | 14.96655 | -7 | -2.5 | -9.551287 | 11.39532 | 200931 |
| 2.467353 | 24.60181 | -6.5 | -3 | -8.77859 | 11.17141 | 157974 |
| 2.465624 | 34.14288 | -6.5 | -2.5 | -8.516298 | 11.30792 | 75221 |
| 2.464132 | 42.46207 | -6.5 | -3 | -8.107101 | 11.46713 | 12871 |
| 3.940044 | 6.494463 | -5 | -2.5 | -6.850049 | 8.632158 | 159359 |
| 3.920908 | 14.93237 | -4.5 | -1.5 | -6.738891 | 9.638292 | 259999 |
| 3.91376 | 24.59291 | -4 | -2 | -6.331322 | 9.770061 | 200826 |
| 3.910582 | 34.12962 | -4 | -1.5 | -6.165928 | 9.950109 | 94508 |
| 3.911752 | 42.43478 | -4 | -2.5 | -6.100883 | 10.56923 | 15627 |
| 5.973475 | 6.30899 | -2.5 | -1 | -3.93609 | 6.679157 | 124143 |
| 5.947416 | 14.87571 | -2 | -0.5 | -3.855116 | 7.593038 | 176658 |
| 5.935386 | 24.57009 | -2 | -0.5 | -3.75843 | 7.967135 | 130968 |
| 5.929262 | 34.09703 | -2.5 | -0.5 | -3.865756 | 8.462518 | 59373 |
| 5.930631 | 42.42386 | -2 | 0.5 | -3.737195 | 8.848928 | 9606 |
| 8.473679 | 6.263705 | -2 | -1.5 | -2.909206 | 5.635937 | 37376 |
| 8.428466 | 14.86537 | -2 | -1 | -2.794891 | 6.27739 | 51263 |
| 8.405581 | 24.56638 | -1.5 | -0.5 | -2.755658 | 6.887471 | 38090 |
| 8.398643 | 34.09077 | -1.5 | -0.5 | -2.789349 | 7.332652 | 17688 |
| 8.417135 | 42.49469 | -1.5 | -1 | -2.571507 | 7.58237 | 2741 |
| 12.38283 | 5.928576 | -1 | -0.5 | -1.336146 | 4.401685 | 54820 |
| 12.36335 | 14.85055 | -0.5 | 0 | -1.091778 | 4.620873 | 68159 |
| 12.34546 | 24.57109 | -0.5 | 0 | -0.898836 | 5.115211 | 48387 |
| 12.33415 | 34.10803 | -0.5 | 0 | -0.796106 | 5.590997 | 21597 |
| 12.29493 | 42.35923 | -0.5 | 0 | -0.901933 | 6.082977 | 3518 |
| 17.37747 | 5.691648 | -0.5 | 0 | -0.628129 | 3.999388 | 40186 |
| 17.35511 | 14.82281 | 0 | 0 | -0.50893 | 4.179274 | 48322 |
| 17.34096 | 24.48245 | 0 | 0.5 | -0.414766 | 4.779402 | 33103 |
| 17.33351 | 34.10130 | 0 | 0 | -0.373912 | 5.167998 | 14712 |
| 17.33278 | 42.34863 | 0 | 1 | -0.386445 | 5.567493 | 2228 |
| 24.65351 | 5.387527 | 0 | 0 | -0.089354 | 3.730998 | 56668 |
| 24.53464 | 14.76977 | 0 | 0.5 | -0.075215 | 3.943362 | 61896 |
| 24.49157 | 24.48757 | 0 | 0.5 | -0.013354 | 4.38043 | 41487 |
| 24.50113 | 34.09296 | 0 | 0 | -0.050458 | 4.883304 | 17886 |
| 24.54165 | 42.39799 | 0 | 0.5 | -0.080075 | 5.687932 | 2941 |
| 38.91114 | 4.866641 | 0.5 | 0.5 | 0.568916 | 3.375527 | 67372 |
| 38.57323 | 14.73106 | 0.5 | 0.5 | 0.455819 | 3.402687 | 61509 |
| 38.44298 | 24.49291 | 0.5 | 0.5 | 0.531074 | 4.031707 | 39518 |
| 38.33975 | 34.11068 | 0.5 | 0.5 | 0.477479 | 4.738723 | 16829 |
| 38.47187 | 42.40413 | 0.5 | 0.5 | 0.366934 | 5.213709 | 2867 |
| 69.10617 | 4.330937 | 1 | 1 | 1.176867 | 2.993901 | 63460 |
| 67.83467 | 14.60966 | 1 | 1 | 1.003142 | 3.086671 | 44561 |
| 67.04486 | 24.38399 | 1 | 1 | 1.064233 | 3.563003 | 25937 |
| 67.37074 | 34.17498 | 1 | 1.5 | 1.019543 | 4.064615 | 10848 |
| 67.06462 | 42.30343 | 1 | 1 | 0.773429 | 4.98562 | 1878 |
| 134.9008 | 3.767374 | 2 | 2 | 2.040394 | 2.91173 | 20139 |
| 129.1826 | 14.39104 | 1.5 | 1.5 | 1.722651 | 3.247738 | 9068 |
| 127.0093 | 24.29037 | 2 | 2 | 1.951822 | 3.891673 | 4556 |
| 129.9621 | 34.42427 | 2 | 2.5 | 1.882984 | 4.288491 | 1910 |
| 131.0391 | 42.25512 | 1.5 | 1 | 1.88427 | 4.567912 | 445 |
One can see that there is no evidence in the data for a "curvature" correction. This may be due to contamination from events where the core locator incorrectly determined the shower core.
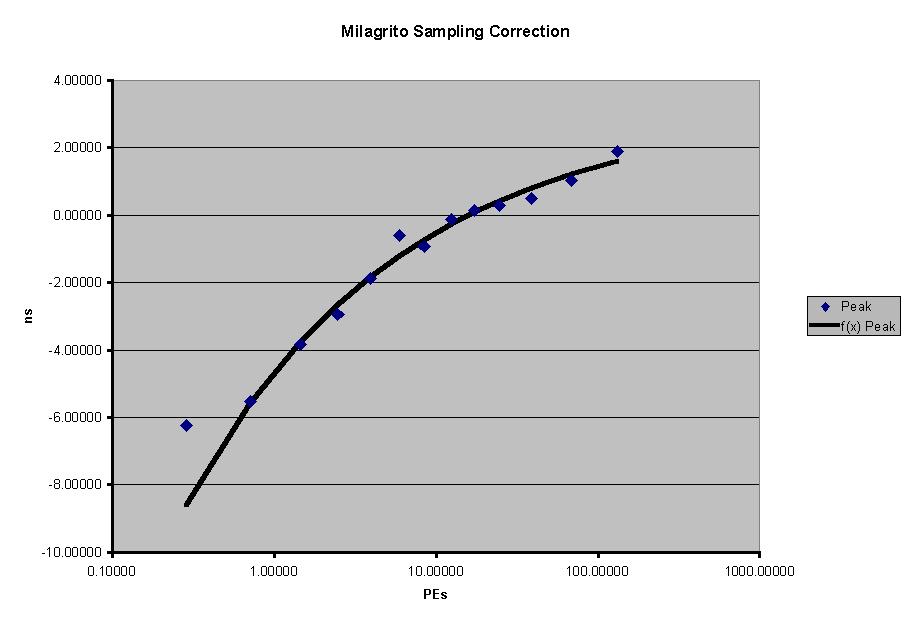
I used the above table to determine the sampling correction (independent of core distance) by averaging over all core distances for each pulse height bin. For this analysis, I chose to correct the peaks (mode) of the Tc distributions to 0.
The black line is the fit and the blue diamonds are the data. The smallest PE bin (0-0.25) was not used in the fit. The fit function is:
![]()
The next step is fitting the sigmas and the RMSís of the residuals as a function of Pes. The blue diamonds are the data and the black line is the fit:
![]()
The first equation is used if Pes < 12.3, the second otherwise.
Finally, I fit the RMS's of the TCHI distributions as a function of Pes.
The blue diamonds are the data and the black line is the fit:
![]()
The Final Fitter:
Once I have the above functional forms for the sampling correction, the sigmas, and the RMS's of the TCHI distributions as a function of pulse height I can begin to perform the angle fitting. There is still a wide selection of options available.
Using DELEO as my guide I arrived at the following choices:
Below is a plot of DELEO, NFIT, DELEO vs. Zenith angle, DELEO vs. NFIT, DELEO for NFIT > 40, and DELEO vs. Zenith angle for NFIT > 40 for the above fitter.
Limitations of Technique:
One can see that for NFIT>40 DELEO looks quite good. However DELEO has only half the counters to work with. Therefore one might expect the fitter itself to do well if NFIT>20. Below I show a plot of the RMS of TCHI distribution (for all PMTs with 10<PES<20) as a function of NFIT. Superimposed on the plot is the function 1/sqrt(NFIT), normalized to large values of NFIT. We see that indeed at an NFIT value of 20, the RMS has a similar behavior to DELEO for NFIT of 40.
Fraction of Showers Fit:
Roughly 90% of all triggers (100 PMT multiplicity requirement) pass the fitting algorithm. It is believed that the failed 10% are not air showers but triggers due to large angle muons. If the additional requirement of NFIT>20 is made, 70% of the fit showers pass. In an attempt to recover some of these events I have modified the above fitting algorithm in the follwoing manner.
Relax:
There are 4 passes through the fitter, at each pass PMTs are excluded/included in the fit based on the DISTANCE = (PMT time - fit time)/(sigma of PMT hit). At each pass the number of PMTs used in the fit is checked. If NFIT < 20 the PE requirement is relaxed. After the first pass if less than 20 PMTs are in the fit the PE requirement is relaxed to 1.5 PEs. After the second pass if there are still less than 20 PMTs in the fit the PE requirement is relaxed to 1 PE. However, at the same time the DISTANCE criteria is made stricter so that only those low PE hits that are consistent with the already fitted plane are used in the next pass. Below I show the resulting NFIT distribution and DELEO distribution.
With this version of the fitter 91% of the triggered events are reconstructed and of these 87% have 20 or PMTs used in the fit. The Deleo distribution (for NFIT > 40) indicates that the angular resolution on this set of events is ~0.5 degrees.
Systematic Offset of Previous Fitter:
The previous online fitter was using timing pedestals derived from the data itself. Peter Nemethy showed atour last collaboration meeting that this should have given rise to a systematic pointing error of 2 degrees due west. The following figures show the angle difference between this version of the fitter and the previous version running online and the projections of that difference along the east-west axis and the north-south axis.
Here are the reconstructed theta and phi distributions:
Conclusions:
I have implemented the laser calibration data and the adc calibration data into the angular reconstruction code. Using a sampling correction only (no curvature correction) that is derived by aligning the peaks in the distributions of the timing residuals, and "optimizing" the PMT selection criteria we can attain an angular resolution of ~0.5 degrees for ~80% of the triggered events.