This page contains all class handouts and other items of interest for students of Physics 116A at the University of California, Santa Cruz.
SPECIAL ANNOUNCEMENTS
This website will be kept live for the remainder of the academic
2019--2020 year. Feel free to consult it while you are taking Physics 116B and C.
Physics 116A: Mathematical Methods in Physics I
I. General Information and Syllabus
The General Information and Syllabus handout is available
in either PDF or Postscript format
[PDF | Postscript]
Some of the information in this handout is reproduced below.
Class Hours
Lectures: Tuesdays and Thursdays, 1:30--3:05 pm, Thimann Lecture Hall 001
Discussion Sections (led by Joseph "Zippy" Connell)
There will be three discussion sections that will take place in ISB
231/235.
Mondays, 4--5:30 pm
Wednesdays, 10:40--11:45 am
Wednesdays, 4--5:30 pm
Instructor Office Hours
Mondays, 2--4 pm.Required Textbook
Mathematical Methods in the Physical Sciences, by Mary L. Boas
The author keeps track of the latest list of errata for her textbook in the following PDF file.
Course Grading and Requirements
45% Weekly Homework (9 1/2 problem sets)
20% Midterm Exam (Tuesday, November 5, 2019, 1:30--3:05 pm)
35% Final Exam (Thursday, December 12, 2019, 12--3 pm)
Homework assignments will be posted on the course website on a weekly basis, and are due each Thursday at the beginning of class. (Due to the Thanksgiving holiday, the final two homework sets will be due on the two Tuesdays following Thanksgiving.) The homework problem sets are not optional. You are encouraged to discuss the class material and homework problems with your classmates and to work in groups, but all submitted problems should represent your own work and understanding. In order that homework can be graded efficiently and returned quickly, there will be a 50% penalty for late homework. This penalty may be waived in special circumstances if you see me before the original due date. Homework solutions will be made available one or two days after the official due date; no late homeworks will be accepted after that.
The midterm and final exams will be held in the same classroom as the lectures. The final exam will be three hours long and cover the complete course material. You must take the final exam to pass the course. You will be permitted to consult the class textbook, your own handwritten notes, and any class handout during the exams.
Course Syllabus
The course syllabus is available in either PDF or Postscript format
[PDF | Postscript]
A snapshot of the course lecture schedule appears below.
The dates given below are approximate.
Brief Course Outline for Physics 116A |
||
|---|---|---|
| TOPIC | Lecture dates | Readings |
| Infinite series and power series | Sept 26, Oct 1, 3, 8 | Boas, Chapter 1 | Complex numbers and complex functions | Oct 10, 15, 17, 22 | Boas, Chapter 2 | Matrices, linear algebra and vector spaces | Oct 24, 29, 31, Nov 7 | Boas, Chapter 3 | Eigenvalue problems and matrix diagonalization | Nov 12, 14, 19 | Boas, Chapter 3 | Ordinary Differential Equations | Nov 21, 26, Dec 3, 5 | Boas, Chapter 8 |
Note: in past years, material on tensors analysis from Boas, Chapter 10 has also been presented in Physics 116A. However, I believe that a superficial discussion of this topic at the expense of a more thorough treatment of the subjects listed above is counterproductive. If time permits, some aspects of tensors will be introduced as they relate to the topics linear algebra covered in this class.
There will be a midterm and final exam:
- Tuesday November 5, 1:30--3:05 pm Midterm exam
- Thursday December 12, 12--3 pm Final exam
II. Disability Statement to Students in Class
UC Santa Cruz is committed to creating an academic environment that supports its diverse student body. If you are a student with a disability who requires accommodations to achieve equal access in this course, please submit your Accommodation Authorization Letter from the Disability Resource Center (DRC) to me privately during my office hours or by appointment, as soon as possible in the academic quarter, preferably within 1 week. I also am open to and want to encourage you to discuss with me ways I/we can ensure your full participation in this course. If you have not already done so, I encourage you to learn more about the many services offered by the DRC. You can visit their website (http://drc.ucsc.edu/index.html), make an appointment, and meet in-person with a DRC staff member. The phone number is 831-459-2089 or email drc@ucsc.edu.III. Computer algebra systems
Although the use of computer algebra is not mandatory in this class, it can be a very effective tool for pedagogy. In addition, if used correctly, it can be an invaluable problem solving tool. Two of the best computer algebra systems available are Mathematica and Maple. There are student versions of both Mathematica and Maple available, which sell for the cost of a typical mathematical physics textbook.IV. Homework Problem Sets and Exams
Problem sets and exams are available in either PDF or Postscript formats.
- Homework Set #1--due: Thursday October 3, 2019 [PDF | Postscript]
- Homework Set #2--due: Thursday October 10, 2019 [PDF | Postscript]
- Homework Set #3--due: Thursday October 17, 2019 [PDF | Postscript]
- Homework Set #4--due: Thursday October 24, 2019 [PDF | Postscript]
- Homework Set #5--due: Thursday October 31, 2019 [PDF | Postscript]
- Midterm Exam---Tuesday November 5, 2019 [PDF | Postscript]
- Homework Set #6--due: Thursday November 7, 2019 [PDF | Postscript]
- Homework Set #7--due: Thursday November 14, 2019 [PDF | Postscript]
- Homework Set #8--due: Thursday November 21, 2019 [PDF | Postscript]
- Homework Set #9--due: Tuesday December 3, 2019 [PDF | Postscript]
- Homework Set #10--due: Monday December 9, 2019 [PDF | Postscript]
- Final Exam---Thursday December 12, 2019 [PDF | Postscript]
V. Practice Problems for the Midterm and Final Exams and their solutions
Practice midterm and final exams can be found here. These should give you some idea as to the format and level of difficulty of the exam. Solutions will be provided two days before the corresponding exam.
- Practice Midterm [PDF | Postscript] and their solutions: [PDF | Postscript]
- Additional midterm exam practice problems [PDF | Postscript] and their solutions: [PDF | Postscript]
- Practice Final Exam [PDF | Postscript] and their solutions: [PDF | Postscript]
- Additional Final Exam practice problems [PDF | Postscript] and their solutions: [PDF | Postscript]
VI. Solutions to Homework Problem Sets and Exams
The homework set and exam solutions are available in PDF format. Solutions will be posted one or two days after the homework is due and after the exams have been completed. There is no password required to view the solutions.
- Solution Set #1 [PDF | Postscript]
- Solution Set #2 [PDF | Postscript]
- Solution Set #3 [PDF | Postscript]
- Solution Set #4 [PDF | Postscript]
- Solution Set #5 [PDF | Postscript]
- Solutions to the Midterm Exam [PDF | Postscript]
- Solution Set #6 [PDF | Postscript]
- Solution Set #7 [PDF | Postscript]
- Solution Set #8 [PDF | Postscript]
- Solution Set #9 [PDF | Postscript]
- Solution Set #10 [PDF | Postscript]
- Solutions to the Final Exam [PDF | Postscript]
VII. Other Class Handouts
1. This is a handout on the alternating series test, with a clarification on the behavior of series that do not meet all the conditions of the test. [PDF | Postscript].
2. Section 11 in Chapter 1 of Boas mentions a number of theorems about power series, although little detail is provided. In this handout, I have elaborated on these theorems. In particular, I state an important result, called Abel's Theorem, that asserts that if a series is convergent at an endpoint of the interval of convergence, then the series must be continuous at this point. [PDF | Postscript].
3. (Optional handout) Applying Abel's theorem incorrectly can lead to apparent paradoxes in the evaluation of power series at the endpoint of its interval of convergence. This handout describes the apparent paradox and its resolution. [PDF | Postscript].
4. (Optional handout) The sum of an infinite series of functions is
pointwise convergent over an interval defined by
a < x < b if the sum is convergent at each point in the interval.
However, the derivative of an infinite pointwise convergent sum of
functions is not always equal to the sum of the derivatives.
Likewise, the integral of an infinite pointwise convergent sum of
functions is not always equal to the sum of the integrals.
It is useful to introduce a stricter notion of convergence called
uniform convergence. Uniformly convergent sums are much better
behaved. All power series
with a radius of convergence R is uniformly convergent over any
closed interval [-r,r], where 0 < r < R. For further details, see the
following class handout , which
distinguishes between these two concepts of a convergent sum of
functions:
[PDF | Postscript].
5. Taylor series can be used to approximate functions. By summing
over a finite number of terms, it is often possible to obtain
a bound on the error made by replacing the function with the sum of
the first N terms of the Taylor series. (The error will depend on
the point at which the function is evaluated.) One such example
is provided by Theorem 14.4 on p. 35 of Boas. A proof of this theorem
and a simple example are provided in this class handout
handout.
[PDF | Postscript].
6. A list of Taylor series for some well known functions is provided
in this handout.
The coefficients of the Maclaurin series for tan(x)
and sec(x) depend on the Bernoulli and Euler numbers, respectively.
Some properties of these numbers are presented.
[PDF | Postscript].
7. Suppose we wish to study the behavior of a function f(x) for
values of x in
the neighborhood of x=a, where a is a real (or complex) number.
We would like to know how f(x) approaches f(a)
as x → a. This handout provides an introduction to
the Big Oh (order) symbol and how to use it in expressing the behavior of
a function.
[PDF | Postscript].
8. In a handout entitled Complex conjugation, Modulus, and Inequalities,
I provide a list of a number of simple identities involving the modulus
and complex conjugate of a complex number. In addition, I list three
useful inequalities involving complex numbers including the famous triangle inequality. An
algebraic proof of the triangle inequality is provided and the
condition under which the inequality reduces to an equality is derived.
[PDF | Postscript].
9. A complex number can be written in polar form as
z=ei θ, where θ is called the principal value of
the argument of z and is denoted by Arg z. One can also define a
multivalued argument function as arg z=Arg z+2πn (where n is any
integer). Details of the properties of arg z and Arg z can be found
in this handout.
[PDF | Postscript].
10. A complex logarithm, exponential and power functions do not
possess many of the simple properties associated with the
corresponding real-valued functions. Ignoring this simple fact can
lead to apparent paradoxes. In these highly detailed (and sometime dense)
notes,
I carefully define the complex logarithm, exponential and
power functions, paying careful attention to distinguish between the
multivalued functions and their single-valued principal value
counterparts.
[PDF | Postscript].
11. (Optional handout)
The inverse trigonometric and the inverse hyperbolic functions are
multivalued functions that can be written in terms of the complex
logarithm. In these comprehensive notes,
I provide a derivation of these expressions.
I also carefully define the (single-valued) principal values of the
inverse trigonometric and the inverse hyperbolic functions
and their branch cuts following
the conventions of Mathematica computer algebra software, and
compare with the standard conventions for the
real-valued inverse functions.
[PDF | Postscript].
12. Given a power series of a complex function f(z) with a radius of
convergence R, the power series converges for |z|< R.
The question of the convergence properies on the circle of convergence
(i.e., for |z|=R) is a delicate one. If certain conditions are
satisfied, then f(z) converges for all |z|=1, with the
possible exception of z=1. The relevant theorem is stated and
a proof is given. Three examples exhibit the theorem in action.
[PDF | Postscript].
13. Numerous problems in linear algebra can be solved by employing
elementary row operations to convert a matrix into its reduced row
echelon form. In this handout entitled Elementary row operations and some applications, explicit
forms for the elementary matrices that correspond to the elementary
row operations are given. The reduced row echelon form is
defined and a procedure for achieving this form is outlined, called
Gauss-Jordan elimination. Using these methods, I
provide a proof that the rank of a matrix is equal to the rank of its
transpose. I also provide details on how to compute
the inverse (if it exists) using Gauss-Jordan elimination.
[PDF | Postscript].
14. In this handout entitled Determinant and the Adjugate, the determinant of an n × n matrix is defined by an explicit formula that consists of a sum of products of matrix elements. This formula is written as a sum over even and odd permutations of indices that represent the row or column of the matrix. The formula can also be rewritten in a more illuminating way by introducing the Levi-Civita symbol. The handout also introduces the adjugate of a matrix and shows how to use it to compute the inverse of a matrix (if it exists). Finally, a proof of Cramer's rule is provided. [PDF | Postscript].
15. This handout, entitled Rotation Matrices in Two, Three, and
Many Dimensions, first shows that n×n matrices
that represent proper rotations are orthogonal with determinant 1 and
improper rotation matrices are orthogonal with determinant -1.
The most general 2×2 proper and improper rotation matrices are
derived. In the case of 3 dimensiosns, the most general forms of the
the proper and improper rotation matrices are exhibited.
A derivation of the most general 3×3 rotation matrix is given in
an optional appendix.
[PDF | Postscript].
16. This handout discusses a number of basic properties of the
characteristic polynomial of a matrix and shows
how the coefficients of the characteristic polynomial are related
to the eigenvalues. A proof is given of the Cayley-Hamilton theorem,
which states that any matrix satisfies its own characteristic
equation. An optional set of appendices provide explicit formulae for
the coefficients of the characteristic polynomial of the matrix in
terms of its elements.
[PDF | Postscript].
17. This handout discusses vector components
(also called coordinates), matrix elements
and changes of basis. Applications to the matrix diagonalization
problem are provided. The implications of the inner product to these
applications are also discussed.
[PDF | Postscript].
18. The eigenvalues and eigenvectors of proper and improper rotation
matrices in two and three dimensions are computed and their
significance is explained in this class handout entitled, Eigenvalues and
eigenvectors of rotation matrices. These notes supplement a
previous class handout entitled, Rotation Matrices in Two, Three, and
Many Dimensions
[PDF | Postscript].
19. First order differential equations that are either exact and/or
separable are easily solved. Non-exact, non-separable first order
differential equations are far more challenging. With some inspired
guesswork, one can often convert a non-exact differential equation
into an exact differential equation by multiplying the original
equation by an integrating factor. Some techniques for finding
integrating factors for first order non-exact differential equations
are presented in this handout.
[PDF | Postscript].
20. The Wronskian has a number of useful applications in the treatment of second order linear differential equations. In these notes, I show how to use the Wronskian to find a second solution to a homogeneous second order linear differential equation if the first solution is known. I also demonstrate how to obtain the particular solution to an imhomogeneous second order linear differential equation if the solutions to the corresponding homogeneous equation are known. A number of examples are provided in this class handout. [PDF | Postscript].
21. Boas shows that one can solve the Euler-Cauchy differential equation by a simple change of variable, which converts the equation into a linear differential equation with constant coefficients (which can be easily solved). In addition to providing some of the details that Boas omitted, I show in these notes that one can obtain the solution to the Euler-Cauchy differential equation directly without preforming the variable change mentioned above. [PDF | Postscript].
VIII. Free online textbooks
1. A very good source for free mathematical textbooks can be found on FreeScience webpage. I can also provide another useful link to a list of free mathematics textbooks here.2. Lecture notes on infinite series written by Vince Vatter (who is a professor of mathematics at the University of Florida) provide an elementary treatment of sequences, infinite series and power series. These notes, which are available here in PDF format, are very readable and provide more details than Chapter 1 of Boas. You will also find additional problems along with some solutions.
3. Infinite sequences and sums are some of the initial topics studied in a mathematical real analysis course. Such a course provides a sophisticated treatment of concepts first learned in calculus. Here, I provide a free textbook by Brian S. Thomson, Judith B. Bruckner and Andrew M. Bruckner, Elementary Real Analysis, taken from http://classicalrealanalysis.info. For this course, I recommend that you peruse Chapters 2, 3, 9 and 10, if you wish to read more about infinite series and power series. These chapters are quite readable for Physics 116A students (even if the rest of the book is somewhat advanced).
4. Sean Mauch (of Caltech) provides a free massive textbook (2321 pages) entitled Introduction to Methods of Applied Mathematics. You may be particularly interested in his treatment of complex numbers. He takes 180 pages to cover the material of Chapter 2 of Boas. I have isolated the two relevant chapters on complex numbers and complex functions to this PDF link. These chapters also provide useful worked out examples.
5. James Nearing also provides a free textbook entitled Mathematical Tools for Physics. This book treats most of the topics of Physics 116A at a similar level of difficulty. Although not as comprehensive as the one by Sean Mauch, you may find some of the presentations enlightening.
6. David A. Santos provides a free textbook on linear algebra which I have uploaded to this website in PDF format. I believe that you will find this quite useful. It covers all the topics of chapters 3 of Boas in greater depth, but at about the same level of sophistication. In addition, it provides many worked out examples.
7. William Chen has a extensive set of lecture notes on linear algebra consisting of twelve chapters on topics, many of which have been treated in Physics 116A. Click on the individual chapter headings to download the pdf versions of each chapter.
8. If you need more practice on problems in matrices and linear algebra, I highly recommend a free textbook by Jim Hefferon entitled Linear Algebra available as a free PDF download along with the answers to exercises. Note that if you save the two files in the same directory, then clicking on an exercise will send you to its answer and clicking on an answer will send you to its exercise.
9. Yet Another free text book on linear algebra by Sergei Treil entitled Linear Algebra Done Wrong can be found here in PDF format. This book is advertised as a first linear algebra course for mathematically advanced students. It is intended for a student who, while not yet very familiar with abstract reasoning, is willing to study more rigorous mathematics than is presented in a "cookbook style" calculus type course. You will have to check out the preface of this book to see why the author chose such a strange title for his opus.
10. You may find the textbook by William F. Trench entitled Elementary Differential Equations quite useful. This book was published previously by Brooks/Cole Thomson Learning, 2001. This free edition is made available courtesy of the author. The author also is providing free of charge the Student Solutions Manual for his book. For more details, check out the following webpage.
11. In Sean Mauch's free massive textbook cited previously above, you may be interested in his treatment of ordinary differential equations. I have isolated five relevant chapters on ordinary differential equations to this PDF link. These chapters also provide useful worked out examples.
IX. Articles of Interest
1. The Internal Revenue Service has used an infinite geometric series to determine the quoted tax withholding rate if an organization chooses to cover the tax on the item being raffled. For more details, check out this short article that appears in the August/September 2019 issue of MAA Focus. [PDF]
2. If the rearrangement of conditionally convergent series strikes your fancy, check out this link for a more in depth discussion of rearranging the alternating harmonic series.
3. There are many proofs that the infinite harmonic series is divergent. Click here for twenty different proofs of this well known theorem. This paper is very elementary and clearly written. Applications of the harmonic series are ubiquitous. For example, see this note written by David Bressoud.
4. Did you ever wonder how to prove that
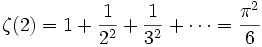 ?
Click
here for
fourteen different proofs of
this result.
If fourteen proofs are too much to handle, try clicking
here for a more modest presentation that
presents six different ways
to sum the series. The latter
presentation is slightly more elementary in style as compared to the former.
?
Click
here for
fourteen different proofs of
this result.
If fourteen proofs are too much to handle, try clicking
here for a more modest presentation that
presents six different ways
to sum the series. The latter
presentation is slightly more elementary in style as compared to the former.
5. A beautifully typeset article (with a pleasing use of colors and photographs) entitled Values of the Riemann zeta function at integers by R.J. Dwilewicz and Jan Minac provides an introduction to some of the mysteries of the Riemann zeta function. In this article, prime numbers, Euler's constant, and the Bernoulli numbers all play a role in the story. The article is quite readable for the most part (you can ignore the more advanced material that occasionally appears) and definitely worth perusing. It can be found here: [PDF].
6. The history of pi is fascinating. Check out this review paper by Peter Borwein, one of the giants in the field of pi research, which is available in PDF format. A slightly older and shorter review by the same author can be found here: [PDF | Postscript].
7. Boas quotes the following important theorem at the bottom of page 154. A matrix can be diagonalized by a unitary similarity transformation if and only if it is normal, i.e. if the matrix commutes with its hermitian conjugate. For a proof of this result along with a pedagogical treatment of normal matrices written especially for physics students, see Philip A. Macklin, Normal Matrices for Physicists, American Journal of Physics 52, 513--515 (1984). If you are logged onto a campus computer, then you can directly download the article here: [PDF].
X. Delving Deeper
1. If you a looking for a gentle introduction into the the mathematics of Boas Chapter 1, look no further than Numbers and Functions: Steps into Analysis, 3rd edition, by R.P. Burn.
2. For a more sophisticated apporach to numbers and functions (and one of my favorite math books of all time), check out Numbers and Functions: From a classical-experimental mathematician’s point of view, by Victor H. Moll. Feel free to skip around this book and pick out topics of interest to you (or perhaps relevant to Physics 116A).
3. Another terrific resource for material on infinite series is Real Infinite Series by Daniel D. Bonar and Michael J. Khoury. For example, did you know that if you start with the (divergent) harmonic series and remove all terms whose denominators contain at least one nine, then the resulting series is convergent?
4. Although addressed to students of computer science, one of the most entertaining textbooks in mathematics is Concrete Mathematics: A Foundation for Computer Science, 2nd edition, by Ronald L. Graham, Donald E. Knuth and Oren Patashnik. Chapter 2 on Sums is the most relevant for Physics 116A, but you will also find many other treasures in the other chapters of the book (including binomial coefficients, Bernoulli numbers, etc.).
5. An introduction to Bernoulli numbers (and Bernoulli polynomials), along with the connection with the finite sum of the first N powers can be found in this nice review by Pascal Sebah and Xavier Gourdon. [PDF | Postscript]
6. If you would like to learn more about Euler's constant, which is denoted by the Greek letter gamma (γ), and its connections to the harmonic series and other areas of mathematics, start with the wikipedia page for the Euler–Mascheroni constant. At a slightly lower level of sophistication, I highly recommend the entertaining book by Julian Havil entitled Gamma: Exploring Euler's Constant. The level of this book is suitable for any calculus student!
7. Pi has been a topic of fascination for generations of
mathematicians. Two of my all time favorite books on this subject are:
• Jörg Arndt and Christoph Haenel, Pi
Unleashed (Springer-Verlag, Berlin, Germany, 2001)
• Pierre Eymard and Jean-Pierre Lafon, The Number Pi
(American Mathematica Society, Providence, RI, 2004)
Note that you can download the book, Pi
Unleashed, in pdf format when connected to
the University network using the link above.
8. The diagonalization of 2×2 matrices is ubiquitous in physics. After a while, I got tired of constantly rederiving the result for special cases. So, I sat down and computed the general diagonalization of a 2×2 matrix A for the most common cases, where A is either normal, hermitian or real symmetric. For good measure, I also worked out two other diagonalizations that were not covered in this class (called singular value decomposition and Autonne-Takagi factorization). Perhpas you may find some of the material in these notes useful. [PDF | PS]
9. Treating the derivative as an operator allows one to quickly solve a variety of differential equations. If you are interested in pursuing these methods further, have a look at this recent article by Wenfeng Chen entitled, Differential Operator Method of Finding A Particular Solution to An Ordinary Nonhomogeneous Linear Differential Equation with Constant Coefficients [PDF]
10. Problems 1 and 4 on the final exam provide two independent techniques for solving homogeneous linear difference equations with constant coefficients. The function F(x) in problem 1 is called a generating function for the sequence of integers 0,1,1,3,5,11,21,43,.... To learn more about this technique, I can recommend an amazing book by Herbert S. Wilf, entitled "Generatingfunctionology." The second edition of this book is available for free in pdf format.
These same techniques used in problem 4 of the final exam can also be used to derive a closed-form expression for the nth integer of the Fibonacci sequence (0,1,1,2,3,5,8,13,21,...), denoted by Fn. The Fibonacci numbers are intimately connected to the golden ratio (sometimes called the golden mean) which is often denoted by φ=(1+√5)/2. Indeed, there is a remarkable formula that states that Fn= [φn-(-φ)-n]/√5, which implies that Fn+1/Fn → φ as n becomes large. To learn more about the Fibonacci numbers and the golden ratio, check out the corresponding Wikipedia links.
11. Treating love affairs as examples of dynamical systems is the brainchild of Steven H. Strogatz, who is the author of Nonlinear Dynamics and Chaos, with Applications to Physics, Biology, Chemistry and Engineering, 2nd edition (Westview Press, Boulder, CO, 2015). A link to this book can be found here. Problem 6 of the final exam was inspired by Section 5.3 of Strogatz's book. I have reproduced the relevant three pages in the link that follows. [PDF]
12. Following up on Strogatz's work on love affairs, J.C. Sprott examined a sequence of dynamical models involving coupled ordinary differential equations describing the time-variation of the love or hate displayed by individuals in a romantic relationship. For more details, check out the following. [PDF | HTML].
13. A more technical treatment of possible models of the dynamics of romantic relationship can be found in a paper by Alessandra Gragnani, Sergio Rinaldi and Gustav Feichtinger, International Journal of Bifurcation and Chaos, Vol. 07, No. 11, pp. 2611--2619 (1997). [HTML]
XI. Other Web Pages of Interest
1. An apocryphal story relates how a nine-year old Carl Friedrich Gauss managed to compute the sum 1+2+3+...+100 in a few seconds. But is the story true? For an attempt to answer this question, check out an article in the May-June, 2006 issue of the American Scientist by Brian Hayes entitled Gauss's Day of Reckoning. A collection of versions of the Gauss anecdote can be found here.
2. An excellent reference book for Taylor series and many other properties of mathematical functions can be found in the Handbook of Mathematical Functions by Milton Abramowitz and Irene A. Stegun, which is freely available on-line. The home page for this resource can be found here. There, you will find links to a frames interface of the book. Another scan of the book can be found here.
3. A reference that updates the classic reference book of Abramowitz and Stegun is the NIST Handbook of Mathematical Functions (published by Cambridge University Press), together with its Web counterpart, the NIST Digital Library of Mathematical Functions (DLMF). This book is the culmination of a project that was conceived in 1996 at the National Institute of Standards and Technology (NIST). The project had two equally important goals: to develop an authoritative replacement for the highly successful Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, published in 1964 by the National Bureau of Standards (M. Abramowitz and I. A. Stegun, editors); and to disseminate essentially the same information from a public Web site operated by NIST. The new Handbook and DLMF are the work of many hands: editors, associate editors, authors, validators, and numerous technical experts. The NIST Handbook covers the properties of mathematical functions, from elementary trigonometric functions to the multitude of special functions. All of the mathematical information contained in the Handbook is also contained in the DLMF, along with additional features such as more graphics, expanded tables, and higher members of some families of formulas.
4. An encyclopedic treatment of linear algebra and the theory and applications of matrices can be found in the Handbook of Linear Algebra, edited by Leslie Hogben (Chapman and Hall/CRC, Boca Raton, FL, 2007). Full access to the electronic version of this book is provided by the UCSC library at the following link.
5. An encyclopedic treatment of ordinary differential equations (1456 pages), which provides a comprehensive treament of many exact solutions and methods can be found in Andrei D. Polyanin, Valentin F. Zaitsev, Handbook of Ordinary Differential Equations: Exact Solutions, Methods, and Problems, 3rd Edition (CRC Press, Boca Raton, FL, 2018). Full access to the electronic version of this book is provided by the UCSC library at the following link.
haber@scipp.ucsc.edu
Last Updated: January 23, 2020

 Source:
Source:  Click here for the
Click here for the 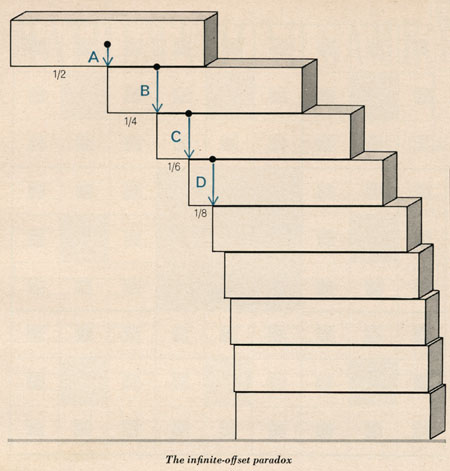 If you stack n bricks on a table,
how far can you make them extend over the edge without toppling?
For bricks of unit length, the answer is given by one-half the
nth harmonic number, i.e. the sum of the series 1/2 + 1/4 + 1/6 + 1/8 +
... + 1/2n.
For more details, click
If you stack n bricks on a table,
how far can you make them extend over the edge without toppling?
For bricks of unit length, the answer is given by one-half the
nth harmonic number, i.e. the sum of the series 1/2 + 1/4 + 1/6 + 1/8 +
... + 1/2n.
For more details, click
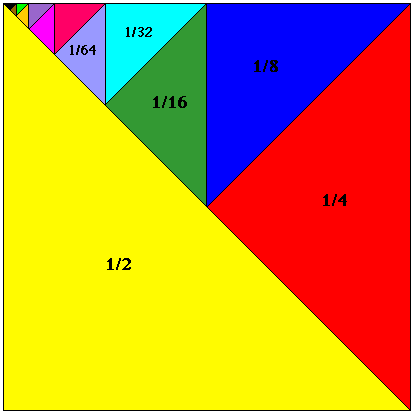
 Some power series you should know by heart.
Some power series you should know by heart.

 This is an excerpt from a 1996 Foxtrot cartoon
created by Bill Amend. On the midterm exam, I asked you
to prove that this series was conditionally convergent.
The actual summation of the series is more difficult.
A solution to this problem (along with the complete Foxtrot cartoon)
can be found
This is an excerpt from a 1996 Foxtrot cartoon
created by Bill Amend. On the midterm exam, I asked you
to prove that this series was conditionally convergent.
The actual summation of the series is more difficult.
A solution to this problem (along with the complete Foxtrot cartoon)
can be found
 Mathematical posters such as this one from RJ:Design can be found
at this
Mathematical posters such as this one from RJ:Design can be found
at this 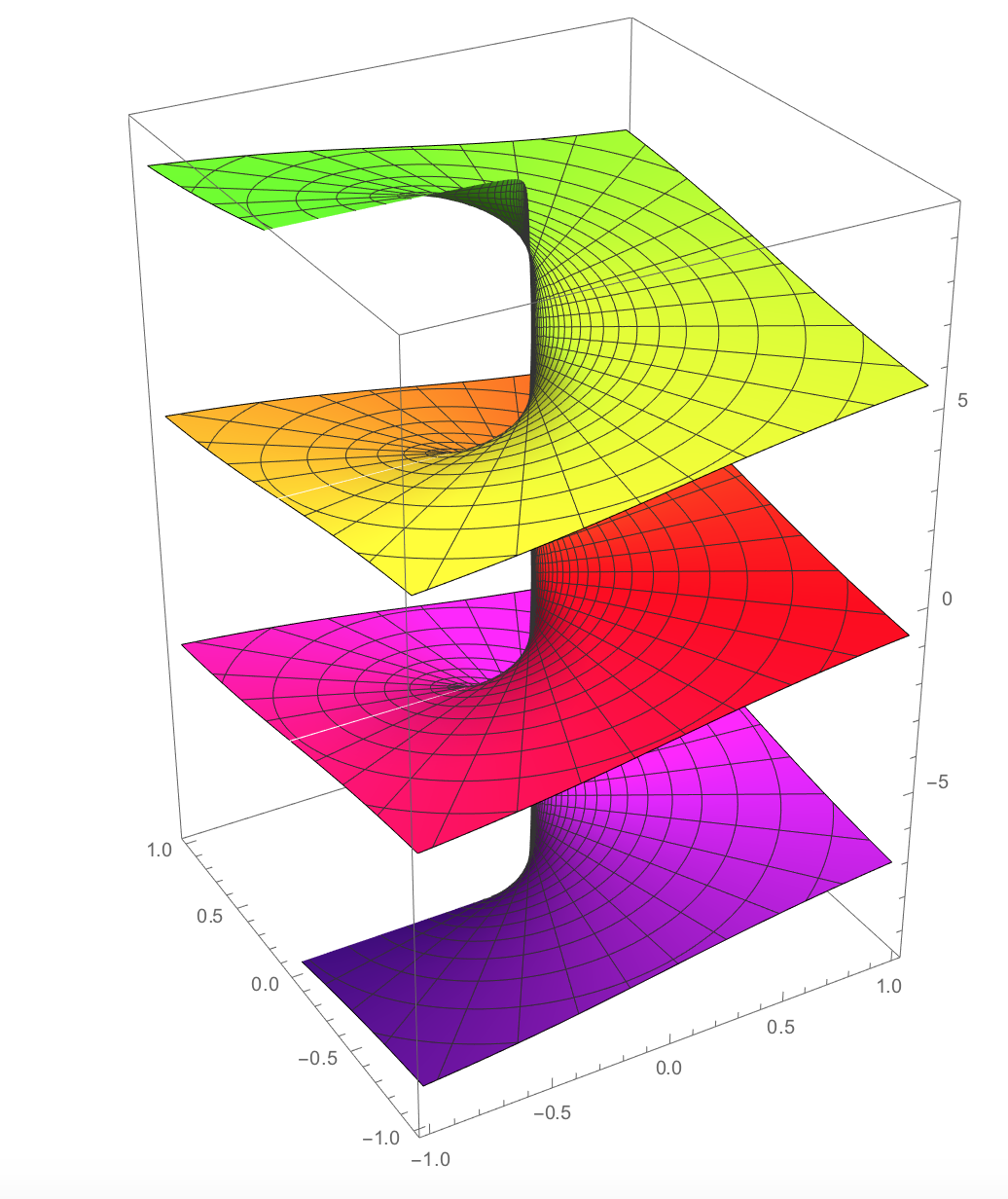 A representation of the complex plane as seen by
the multivalued complex logarithm. This is the Riemann
surface of ln(z). Taken from this
A representation of the complex plane as seen by
the multivalued complex logarithm. This is the Riemann
surface of ln(z). Taken from this
 The matrix has you. Click
The matrix has you. Click
 Hollywood seems to have a thing for linear algebra.
Hollywood seems to have a thing for linear algebra.
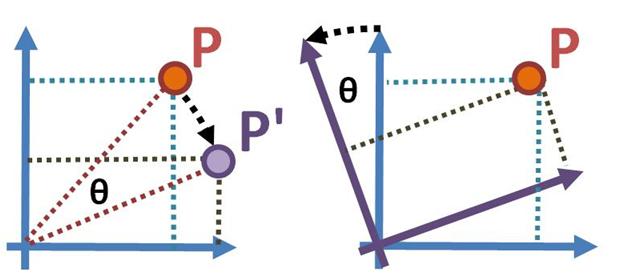 In the active transformation (left), point P moves relative to the
coordinate frame to location P', while the coordinate frame remains
unchanged (in this case, the position of P has rotated clockwise by
angle θ), while in a passive transformation (right), point P is
observed in two different coordinate frames (pictured rotated relative
to one another by angle θ) The coordinates of P' in the active case
are the same as the coordinates of P in the rotated frame in the
passive case if the rotation of P is clockwise and the rotation of the
axes is counterclockwise. (Reference:
In the active transformation (left), point P moves relative to the
coordinate frame to location P', while the coordinate frame remains
unchanged (in this case, the position of P has rotated clockwise by
angle θ), while in a passive transformation (right), point P is
observed in two different coordinate frames (pictured rotated relative
to one another by angle θ) The coordinates of P' in the active case
are the same as the coordinates of P in the rotated frame in the
passive case if the rotation of P is clockwise and the rotation of the
axes is counterclockwise. (Reference:
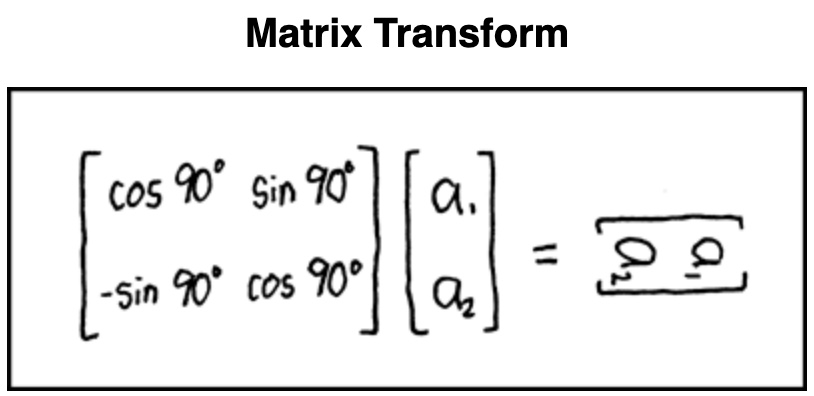 Source:
Source:  Source:
Source:  Suppose you made a different basis choice at each point
in space. Then, your landscape might look like the
famous lithograph by M.C. Escher above entitled Print Gallery.
Escher was also fond of mirror reflecions (see below).
Suppose you made a different basis choice at each point
in space. Then, your landscape might look like the
famous lithograph by M.C. Escher above entitled Print Gallery.
Escher was also fond of mirror reflecions (see below).
 For more information
on Escher and his work, check out the official
For more information
on Escher and his work, check out the official

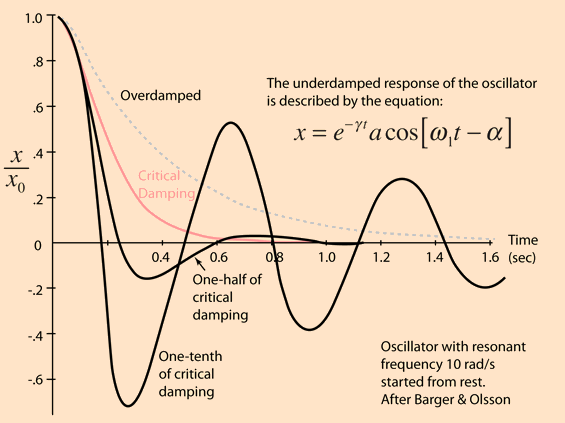 Damped harmonic motion.
Damped harmonic motion.
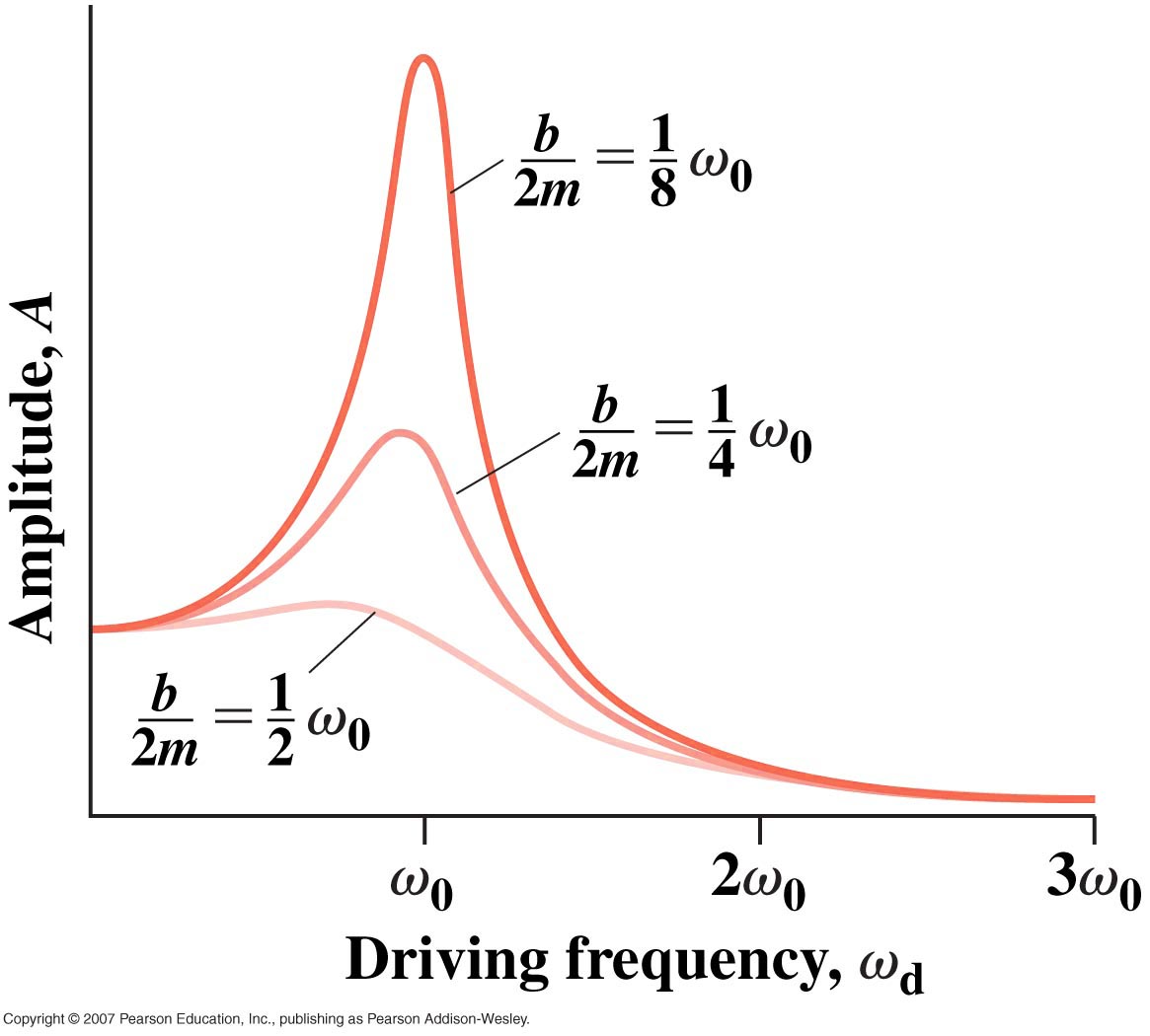 Resonant behavior due to a driven external harmonic source.
Resonant behavior due to a driven external harmonic source.
 In June, 2012, when I was visiting the Palace of Versailles, located 10 miles
west-southwest of Paris, I came across a statue of Pierre-Simon Laplace
(1749--1827). He is among the few scientists honored at the Palace.
In June, 2012, when I was visiting the Palace of Versailles, located 10 miles
west-southwest of Paris, I came across a statue of Pierre-Simon Laplace
(1749--1827). He is among the few scientists honored at the Palace.