Physics 139B Home Page---Fall 2009
This page contains copies of the class handouts, and other
pertinent items of
interest for the U.C. Santa Cruz Physics 139B class.
SPECIAL ANNOUNCEMENTS
 The course grades
and final exam scores are listed by student ID
numbers in this pdf file.
The relevant histograms are posted below.
The course grades
and final exam scores are listed by student ID
numbers in this pdf file.
The relevant histograms are posted below.
Final exam solutions are posted to Section III of this website. The
graded exams are available for pick-up in my office any time this week.
I will be in my office most of the week in the afternoons (excluding
Wednesday).
Have a great winter holiday break---you earned it!!!
The distributions of the final course grades
and the final exam scores are shown in the histograms below:
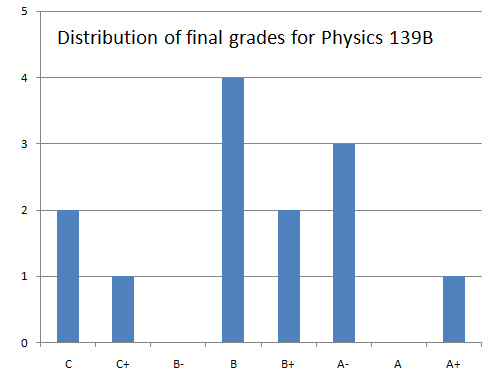
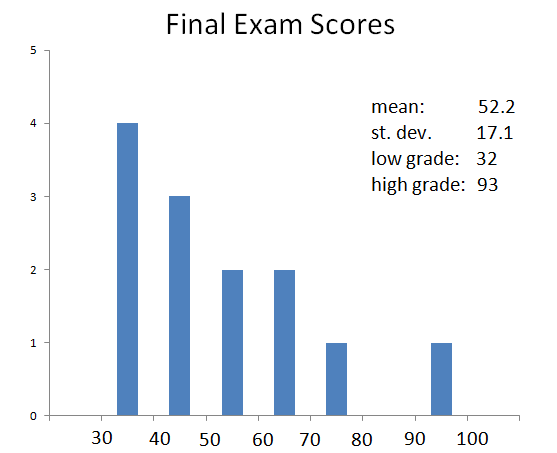
Table of Contents
I. General Information and Syllabus
The General Information and Syllabus handout is available
in either PDF or Postscript format
[PDF | Postscript]
Some of the information in this handout is reproduced here.
General Information |
| Instructor | Howard Haber |
| Office | ISB 326 |
| Phone | 459-4228 |
| Office Hours | Mondays and Tuesdays 2--3 pm |
| e-mail |
haber@scipp.ucsc.edu |
Class Hours
Lectures: Tuesdays and Thursdays, 12:00--1:45 pm, ISB 231
Required Textbook
Introductory Quantum Mechanics, 4th Edition by
Richard L. Liboff
Course Grading and Requirements
40% Homework (5 problem sets)
25% Midterm Exam (Thursday October 29, 2009, 12--1:45 pm)
35% Final Exam (Wednesday, December 9, 2009, 12--3 pm)
Homework assignments will be due on every second Thursday of the
academic quarter starting with the first assignment that is due
on Thursday October 8, 2009.
The homework problem sets are not optional.
You are encouraged to discuss the class material and homework
problems with your classmates and to work in groups, but all
submitted problems should represent your own work and understanding.
The final exam will be held in ISB 231.
This exam will be three hours long and cover the complete course
material. You must take the final exam to pass the course.
You will be permitted to consult the class textbook, your own
handwritten notes, and any class handout during the final exam.
Course Syllabus
- Elements of matrix mechanics [Liboff, sections 11.1--11.5]
- Introduction to spin [Liboff, sections 11.6--11.9]
- Addition of angular momentum [Liboff, sections 9.4, 9.5, 11.10]
- Quantum mechanics in an external electromagnetic field
[Liboff, section 10.4 and handout]
- Time-independent perturbation theory [Liboff, sections 13.1--13.3]
- Applications to atomic and molecular physics
[Liboff, sections 12.1--12.7]
- Time-dependent perturbation theory [Liboff, sections 8.8, 13.5--13.8]
- Quantum theory of scattering [Liboff, sections 14.1--14.6]
- Quantum theory of radiation [Liboff, sections 10.7, 13.9]
Back to the Top
II. Problem Sets and Exams
Problem sets and exams are available in either PDF or Postscript formats.
- Problem Set #1--due: Thursday, October 8, 2009
[PDF | Postscript]
- Problem Set #2--due: Thursday, October 22, 2009
[PDF | Postscript]
- Midterm Exam: Thursday, October 29, 2009
[PDF | Postscript]
- Problem Set #3--due: Thursday, November 5, 2009
[PDF | Postscript]
- Problem Set #4--due: Thursday, November 19, 2009
[PDF | Postscript]
- Problem Set #5--due: Thursday, December 3, 2009
[PDF | Postscript]
- Final Exam: Wednesday, December 9, 2009
[PDF | Postscript]
Back to the Top
III. Solutions to Problem Sets and Exams
The problem set and exam solutions
are available in either PDF or postscript formats.
Back to the Top
IV. Other Class Handouts
Class handouts are available in either PDF or postscript formats.
-
I present the calculation of the ground state energy of the helium
atom using the variational principle. A trial wave function is
presented that depends on a parameter Z, and then
the expectation value of the Hamiltonian with respect to the trial
wave function is evaluated as a function of Z. Details of all the
steps in the calculation are provided (along with a number of
integration tricks) here:
[PDF | Postscript]
-
In the computation of the fine structure of hydrogen, we need to
evaluate the expectation values <1/r^n> (n=1,2,3) with respect
to the hydrogen atom radial wave functions. A clever way of doing
this is provided by Supplement 8A to Gasiorowicz's textbook
(see the following item), which can be found here:
[PDF].
-
The book by Stephen Gasiorowicz, Quantum Physics, 3rd Edition
(John Wiley & Sons, Inc., Hoboken, NJ, 2003) includes free
supplemental material on the Wiley
website. Here, I provide Gasiorowicz's Supplement 16A on the
Aharonov-Bohm effect
[PDF].
-
As Liboff presents only a minimal discussion of the Schrodinger
equation for a charged particle in an external electromagnetic field,
I have written up some more detailed notes on this topic, which
can be found here:
[PDF | Postscript]
-
A nice set of notes by Frank Porter of Caltech
discusses the fundamental role of the electromagnetic vector potential
and the Aharonov-Bohm effect. These note can be found here:
[PDF | Postscript]
Solutions to the problems given at the end of Porter's notes can be
found here:
[PDF | Postscript]
-
A table of Clebsch-Gordon
coefficients is provided courtesy of the Review of of Particle
Physics, published by the Particle Data Group in Physics Letters
B667 (2008) 1--1340.
[PDF]
-
A nice review of vectors and matrices has been provided courtesy of
Michael Dine and can be found here:
[PDF | Postscript]
Back to the Top
V. Articles of Interest
-
In 1977, J.D. Jackson gave a colloquium in which he explained the
connection between the fundamental intrinsic magnetic dipole moment
and the hyperfine structure of the s-states of the hydrogen atom.
His derivation differs somewhat from the one I gave in class, but
of course the results are the same. Jackson provided a writeup of
his colloquium as a CERN Yellow Report (CERN 77-17), which you can
find here: [PDF]
-
The following paper shows how to add two
spin-1/2 angular momenta by representing each spin as a vector
lying in three-dimensional space, but with a vector addition law that takes
into account the quantum mechanical fluctuations.
[PDF | Postscript]
-
A more sophisticated treatment of the graphical representation for the
quantum mechanical addition of two angular momenta can be found
here: [PDF]
Back to the Top
haber@scipp.ucsc.edu
Last Updated: December 12, 2009







