This is the professional website of Howard Haber, Distinguished Professor of Physics at the University of California, Santa Cruz.
RECENT NEWS
 August 20, 2025: The
Santa Cruz Institute for Particle Physics is hosting the 32nd annual
Conference on Supersymmetry and Unification of Fundamental
Interactions, known as SUSY 2025,
from August 18--23, 2025. The aim of the conference is to review and discuss recent
research related to supersymmetric theories and other approaches to
physics beyond the Standard Model in all aspects, including formal
theory, phenomenology, experiment, astroparticle physics and
cosmology. The SUSY 2025 conference photo was taken today
at the end of the morning session.
August 20, 2025: The
Santa Cruz Institute for Particle Physics is hosting the 32nd annual
Conference on Supersymmetry and Unification of Fundamental
Interactions, known as SUSY 2025,
from August 18--23, 2025. The aim of the conference is to review and discuss recent
research related to supersymmetric theories and other approaches to
physics beyond the Standard Model in all aspects, including formal
theory, phenomenology, experiment, astroparticle physics and
cosmology. The SUSY 2025 conference photo was taken today
at the end of the morning session.


August 15, 2025: My paper in collaboration with Sergio Carrolo, Luis Lourenco, and Joao P. Silva, entitled Extending the symmetries of the generalized CP-symmetric 2HDM scalar potential to the Yukawa sector, was published today in Physical Review D. A link to this paper can be found in Section II of this website.
There are only six independent types of symmetry-constrained scalar potentials in the two Higgs doublet model (2HDM). For example, the scalar sector symmetry known as Z2⊗Π2, generated by the simultaneous application of two independent symmetries acting on the scalar fields, and the generalized CP symmetry known as GCP2 yield equivalent 2HDM scalar potentials. A similar situation arises for the scalar sector symmetries known as U(1)⊗Π2 and GCP3, respectively. In this paper, we show that this "degeneracy" remains when the definitions of the corresponding symmetries are extended to the Yukawa sector with three quark generations. Moreover, we find that this result is a peculiarity of a Yukawa sector with three quark generations. In particular, with two quark generations, we find that models based on the extension of Z2⊗Π2 to the Yukawa sector are inequivalent with those based on GCP2.
August 13, 2025: The Pre-SUSY School
2025 is a week of pedagogical lectures aimed at graduate
students and early career postdocs that takes place one week prior
to the 2025 Conference on Supersymmetry and Unification of
Fundamental Interactions (SUSY-2025). This year's Pre-SUSY school
is hosted by the Santa Cruz Institute for Particle Physics from
August 11--15, 2025. The Pre-SUSY 2025 group photo was taken today
at the end of the morning session.


August 12, 2025: An erratum to my paper in collaboration with Pedro Ferreira, entitled RG-stable parameter relations of a scalar field theory in absence of a symmetry, was published today in The European Physical Journal C. A link to this erratum can be found in Section II of this website.
July 9, 2025: Physics Today published an article today entitled Conference organizers, potential participants fault US policies for falling attendance. A link to this article can be found here. I am quoted twice in the article. The article ends with the following sentences:
The threatened funding cuts will significantly reduce the number of research projects and the number of students and early-career researchers who can enter STEM fields, notes Santa Cruz’s Haber. If they materialize, he says, “it will decimate science research and innovation in the US. It will take a generation to repair.”
June 10, 2025: My talk entitled RG-stable parameter relations of a scalar field theory in absence of a symmetry, given at the 7th International Workshop on "Higgs as a Probe of New Physics" (HPNP2025) at Osaka University, in Osaka, Japan, has been posted to Section VII of this website.
May 20, 2025: Today, I gave the SCIPP seminar entitled RG-stable parameter relations of a scalar field theory in absence of a symmetry [PDF]
May 15, 2025: My paper in collaboration with Pedro Ferreira, entitled RG-stable parameter relations of a scalar field theory in absence of a symmetry, was published today in The European Physical Journal C. A link to this paper can be found in Section II of the academic website.
The stability of tree-level relations among the parameters of a quantum field theory with respect to renormalization group (RG) running is typically explained by the existence of a symmetry. We have examined a toy model of a quantum field theory of two real scalars in which a tree-level relation among the squared-mass parameters of the scalar potential appears to be RG-stable without the presence of a corresponding underlying symmetry. The stability of this parameter relation with respect to RG running can be explained by complexifying the original scalar field theory. It is then possible to exhibit a symmetry that guarantees the relations of relevant beta functions of squared-mass parameters of the complexified theory. We can then show that the RG-stability of the parameter relations of the original real scalar field theory is inherited from the symmetry of the corresponding complexified theory.
May 1, 2025: My talk entitled Higgs physics at future e+e- colliders, given at the Corfu2025 Workshop on Future Accelerators at Mon-Repos in Corfu, Greece, has been posted to Section VII of this website.
April 15, 2025: My paper in collaboration with Sumit Banik, Guglielmo Coloretti, and Andreas Crivellin, entitled Correlating EDMs and A→γγ in the 2HDM in light of the diphoton excesses at 95 GeV and 152 GeV, was published today in Physical Review D. A link to this paper can be found in Section II of this website.
Correlations between Higgs boson decays to photons with electric dipole moments (EDMs) in two-Higgs-doublet models are examined. It is shown that CP-violating effects in the scalar potential can lead to a sizable branching ratio of A (the mainly CP-odd Higgs boson) to photons via a charged Higgs loop. The same CP-violating interaction also generates non-zero EDMs for the electron, the neutron, and the proton. While the proposed mechanism holds in general, we illustrate it for the cases of mA= 95 GeV and mA= 125 GeV. In either case, it is found that the corresponding diphoton excess observed at the LHC can be explained via A
→γγ while being consistent with the experimental bound for the electron EDM in regions of parameter space that can be tested with future neutron and proton EDM measurements.March 28 2025: My paper in collaboration with Sergio Carrolo, Luis Lourenco, and Joao P. Silva, entitled Extending the symmetries of the generalized CP-symmetric 2HDM scalar potential to the Yukawa sector, was posted today on the arXiv. A link to this paper can be found in Section II of this website.
There are only six independent types of symmetry-constrained scalar potentials in the two Higgs doublet model (2HDM). For example, the scalar sector symmetry known as Z2⊗Π2, generated by the simultaneous application of two independent symmetries acting on the scalar fields, and the generalized CP symmetry known as GCP2 yield equivalent 2HDM scalar potentials. A similar situation arises for the scalar sector symmetries known as U(1)⊗Π2 and GCP3, respectively. In this paper, we show that this "degeneracy" remains when the definitions of the corresponding symmetries are extended to the Yukawa sector with three quark generations. Moreover, we find that this result is a peculiarity of a Yukawa sector with three quark generations. In particular, with two quark generations, we find that models based on the extension of Z2⊗Π2 to the Yukawa sector are inequivalent with those based on GCP2.
March 13, 2025: My presentation to Physics 205 can be found in Section V of this website.
March 10, 2025: The Santa Cruz Institute for Particle Physics (SCIPP) will be hosting the 32nd International Conference on Supersymmetry and Unification of Fundamental Interactions (SUSY 2025) from August 18--23, 2025. In the tradition of past SUSY Conferences, during the week prior to the main SUSY 2025 conference, SCIPP is hosting the Pre-SUSY School 2025, a week of pedagogical lectures aimed at graduate students and early career postdocs from August 11--15, 2025. The webpages for the SUSY 2025 conference and the Pre-SUSY School are now live.
February 28, 2025: Today I posted a short note to Section VI of the academic website entitled The Hamiltonian of a free Majorana fermion field. In these notes, the quantum Hamiltonian of a free Majorana fermion field in 3+1 spacetime dimensions is expressed as a sum over Fourier modes. The full details of the calculation are provided. The computation is presented first using the four-component spinor formalism. The computation is then repeated using the two-component spinor formalism.
February 18, 2025: My paper in collaboration with Pedro Ferreira, entitled RG-stable parameter relations of a scalar field theory in absence of a symmetry, was posted on the arXiv. A link to this paper can be found in Section II of this website.
The stability of tree-level relations among the parameters of a quantum field theory with respect to renormalization group (RG) running is typically explained by the existence of a symmetry. We have examined a toy model of a quantum field theory of two real scalars in which a tree-level relation among the squared-mass parameters of the scalar potential appears to be RG-stable without the presence of an appropriate underlying symmetry. The stability of this relation with respect to RG running can be explained by complexifying the original scalar field theory. It is then possible to exhibit a symmetry that guarantees the relations of relevant beta functions of squared-mass parameters of the complexified theory. Among these relations, we can identify equations that are algebraically identical to the corresponding equations that guarantee the stability of the relations among the squared-mass parameters of the original real scalar field theory where the symmetry of the complexified theory is no longer present.
December 31, 2024: The 2025 Particle Physics conference schedule has been posted to Section VIII of this website. Although not intended to be comprehensive, it covers many conferences that overlap with my research interests.
 Listings of older news items are stored
here.
Listings of older news items are stored
here.
I. Research
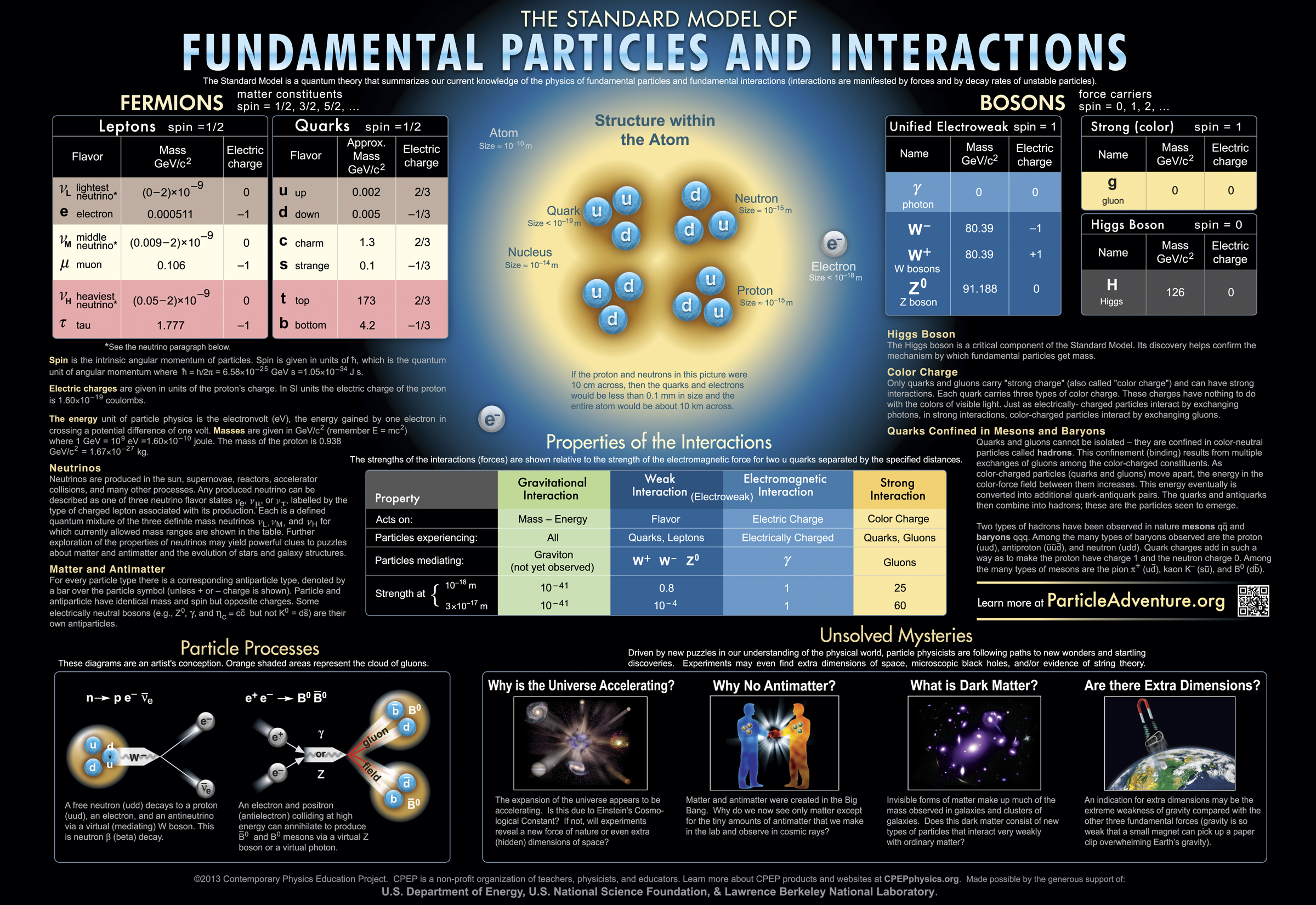
The basic themes underlying my research program involve the study of: (i) the dynamics responsible for electroweak symmetry breaking; (ii) the theory and phenomenology of Higgs bosons; (iii) TeV-scale supersymmetry as a framework for incorporating a weakly-coupled Higgs sector; (iv) the phenomenology of signals for new physics beyond the Standard Model at the Large Hadron Collider (LHC) and future colliders; and (v) connections of low-energy phenomena with fundamental scales that lie beyond the TeV scale (e.g. lepton number violation and implications for neutrino masses).
After more then ten years after the discovery of the Higgs boson in 2012 at the Large Hadron Collider (LHC), many properties of this spin-zero particle have been measured. These results have profound implications for the dynamics of electroweak symmetry breaking and the possible structure of new physics that may lie beyond the Standard Model (SM) of particle physics. For example, most approaches to physics beyond the SM include extended Higgs sectors. Present Higgs data suggest that the properties of one of the scalars of the Higgs sector (identified with the observed Higgs boson) must have properties that closely approximate that of the SM Higgs boson. This constraint in turn imposes important constraints on any SM extension. The two-Higgs doublet model (2HDM) is a convenient theoretical laboratory for the study of extended Higgs sectors. Indeed, the two doublet extended Higgs sector is a key component of the simplest supersymmetric extension of the SM.
The theoretical structure and phenomenological profile of the 2HDM has attracted much attention in recent years. Starting with a seminal paper in collaboration with Sacha Davidson published in 2005, my work has advocated the importance of a basis-independent treatment of the 2HDM. During the past few years, I have focused on the relevance of the so-called decoupling and alignment limits of the 2HDM in which one of scalars closely resembles the SM Higgs boson. The basis-independent technology provides a very powerful and simple framework for studying and interpreting these limits.
If new physics beyond the SM emerges at the LHC, it will be essential
to develop techniques for measuring new particle interaction strengths at
high energy colliders. By detecting relations among various independent
couplings, one can ascertain underlying symmetries and distinguish
among different theoretical interpretations of the new physics. For example,
with sufficient precision, it will be possible to provide convincing
evidence for or against a supersymmetric interpretation of new
fundamental physics phenomena. A precision Higgs program at the LHC
and at a future collider
can also provide important clues as to what may lie beyond the Standard Model.
II. Publications
All my profession publications can be found here on the INSPIRE HEP database.
Most of my professional publications since 1992 are stored on the e-print archive hosted by arXiv.org. PDF and Postscript versions of the stored papers can be found here. My top cited publications according to Google Scholar can be found here.
Links to my most recent preprints:
-
Supersymmetry, Part I (Theory)
Ben Allanach, Howard E. Haber. Jan 8, 2024. 46 pp.
e-Print: arXiv:2401.03827 [hep-ph] | PDF
Links to my 2025 publications:
-
Extending the symmetries of the generalized CP-symmetric 2HDM scalar potential to the Yukawa sector
Sergio Carrolo, Howard E. Haber, Luis Lourenco, Joao P. Silva. Mar 28, 2025. 36 pp.
Published in Phys. Rev. D 112, 035024 (2025)
DOI: 10.1103/pkmr-l9px
Published version: [PDF]
e-Print: arXiv:2503.21387 [hep-ph] | PDF
-
RG-stable parameter relations of a scalar field theory in absence of a symmetry
Howard E. Haber, Pedro M. Ferreira. Feb 18, 2025. 27 pp.
Published in Eur. Phys. J. C 85, 541 (2025), Erratum-ibid. C 85, 867 (2025)
DOI: 10.1140/epjc/s10052-025-14148-3, 10.1140/epjc/s10052-025-14570-7
Published version: [PDF] [Erratum]
e-Print: arXiv:2502.11011 [hep-ph] | PDF
-
Correlating A→γγ with EDMs in the 2HDM in light of the diphoton excesses at 95 GeV and 152 GeV
Sumit Banik, Guglielmo Coloretti, Andreas Crivellin, Howard E. Haber. Nov 30, 2024. 13 pp.
Published in Phys. Rev. D 111, 075021 (2025)
DOI: 10.1103/PhysRevD.111.075021
Published version: [PDF]
e-Print: arXiv:2412.00523 [hep-ph] | PDF
Links to my 2024 publications:
-
Explicit form for the most general Lorentz transformation revisited
Howard E. Haber. Dec 20, 2023. 27 pp.
Published in Symmetry 2024, 16, 1155
DOI: 10.1016//10.3390/sym16091155
Published version: [PDF]
e-Print: arXiv:2312.12969 [physics.class-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
Abstract and PDF from arXiv.org; Journal Server -Symmetry
-
Classes of complete dark photon models constrained by Z-Physics
Miguel P. Bento, Howard E. Haber, Joao P. Silva. Nov 10, 2023. 7 pp.
Published in Phys. Lett. B 850 (2024) 138501
DOI: 10.1016/j.physletb.2024.138501
Published version: [PDF]
e-Print: arXiv:2311.04976 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
Abstract and PDF from arXiv.org; Journal Server - Phys.Lett.
Links to my 2023 publications:
-
Higgs Boson Physics: The View Ahead
Howard E. Haber (UC, Santa Cruz). July 24, 2023. 9 pp.
Published in Letters in High Energy Physics, LHEP-451 (2023)
DOI: 10.31526/LHEP.2023.451
Published version: [PDF]
e-Print: arXiv:2210.00449 [hep-ph] | PDF
References | BibTeX | LaTeX(US) | LaTeX(EU) | Harvmac | EndNote
Abstract and PDF from arXiv.org; Journal Server - LHEP
-
Tree-level Unitarity in SU(2)L×U(1)Y×U(1)Y' Models
Miguel P. Bento, Howard E. Haber, Joao P. Silva. Jun 2, 2023. 28 pp.
Published in JHEP 10 (2023) 083
DOI: 10.1007/JHEP10(2023)083
Published version: [PDF]
e-Print: arXiv:2306.01836 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
Abstract and PDF from arXiv.org; Journal Server - JHEP
-
Accommodating Hints of New Heavy Scalars in the Framework of the Flavor-Aligned Two-Higgs-Doublet Model
Joseph M. Connell, Pedro M. Ferreira, Howard E. Haber. Feb 27, 2023. 48 pp.
SCIPP-22/02
Published in Phys.Rev. D 108, 055031 (2023)
DOI: 10.1103/PhysRevD.108.055031
Published version: [PDF]
e-Print: arXiv: 2302.13697 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
Abstract and PDF from arXiv.org; Journal Server - Phys.Rev
Links to my 2022 publications:
-
P-even, CP-violating Signals in Scalar-Mediated Processes
Howard E. Haber, Venus Keus, Rui Santos. Jun 20, 2022. 58 pp.
DIAS-STP-22-02 and SCIPP-22/01
Published in Phys.Rev. D 106, 095038 (2022)
DOI: 10.1103/PhysRevD.106.095038
Published version: [PDF]
e-Print: arXiv:2206.09643 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
Abstract and PDF from arXiv.org; Journal Server - Phys.Rev
Links to my 2021 publications:
-
Exceptional regions of the 2HDM parameter space
Howard E. Haber, Joao P. Silva. Feb 14, 2021. 97 pp.
CFTP/21-001 and SCIPP-21/01
Published in Phys.Rev. D 103, 115012 (2021), Erratum-ibid. D105 (2022) 119902
DOI: 10.1103/PhysRevD.103.115012, 10.1103/PhysRevD.105.119902
Published version: [PDF] [Erratum]
e-Print: arXiv:2102.07136 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract and PDF from arXiv.org; Journal Server - Phys.Rev
-
A natural mechanism for approximate Higgs alignment in the 2HDM
Patrick Draper, Andreas Ekstedt, Howard E. Haber. Nov 26, 2020. 51 pp.
SCIPP-20/03
Published in JHEP 05 (2021) 235
DOI: 10.1007/JHEP05(2021)235
Published version: [PDF]
e-Print: arXiv:2011.13159 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract and PDF from arXiv.org; Journal Server - JHEP
-
A tale of three diagonalizations
Howard E. Haber. Sep 6, 2020. 27 pp.
Published in Int.J.Mod.Phys. A36 (2021) 2130002
DOI: 10.1142/S0217751X21300027
Published version: [PDF]
e-Print: arXiv:2009.03990 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract and PDF from arXiv.org; Journal Server - Int.J.Mod.Phys.
-
Useful relations among the generators in the defining and adjoint representations of SU(N)
Howard E. Haber. Dec 31, 2019. 11 pp.
Published in SciPost Phys. Lect. Notes 21 (2021)
DOI: 10.21468/SciPostPhysLectNotes.21
Published version: [PDF]
e-Print: arXiv:1912.13302 [math-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract and PDF from arXiv.org
Links to my 2020 publications:
-
Basis-independent treatment of the complex 2HDM
Rafael Boto, Tiago V. Fernandes, Howard E. Haber, Jorge C. Romao, Joao P. Silva. Jan 6, 2020. 65 pp.
CFTP/19-032 and SCIPP-19/01
Published in Phys.Rev. D 101, 055023 (2020)
DOI: 10.1103/PhysRevD.101.055023
Published version: [PDF]
e-Print: arXiv:2001.01430 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract and PDF from arXiv.org; Journal Server - Phys.Rev
Links to my 2019 publications:
-
Symmetries and Mass Degeneracies in the Scalar Sector
Howard E. Haber, O.M. Ogreid, P. Osland, M.N. Rebelo. Aug 26, 2018. 43 pp.
SCIPP-18/04
Published in JHEP 01 (2019) 042
DOI: 10.1007/JHEP01(2019)042
Published version: [PDF]
e-Print: arXiv:1808.08629 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract and
PDF from
arXiv.org; Journal Server
- JHEP
Links to my 2018 publications:
-
Heavy Higgs boson decays in the alignment limit of the 2HDM
Bohdan Grzadkowski, Howard E. Haber, Odd Magne Ogreid, Per Osland. Aug 4, 2018. 44 pp.
SCIPP-18/05
Published in JHEP 12 (2018) 056
DOI: 10.1007/JHEP12(2018)056
Published version: [PDF]
e-Print: arXiv:1808.01472 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract and PDF from arXiv.org; Journal Server - JHEP
-
Multi-Higgs doublet models: the Higgs-fermion couplings and their sum rules
Miguel P. Bento, Howard E. Haber, J.C. Romao, Joao P. Silva. Aug 21, 2018. 24 pp.
SCIPP-18/06
Published in JHEP 10 (2018) 143
DOI: 10.1007/JHEP10(2018)143
Published version: [PDF]
e-Print: arXiv:1808.07123 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract and
PDF from
arXiv.org; Journal Server
- JHEP
Links to my 2017 publications:
-
Multi-Higgs doublet models: physical parametrization, sum rules and unitarity bounds
Miguel P. Bento, Howard E. Haber, J.C. Romao, Joao P. Silva. Aug 30, 2017. 66 pp.
CFTP-17-005, SCIPP-17/10
Published in JHEP 11 (2017) 095
DOI: 10.1007/JHEP11(2017)095
Published version: [PDF]
e-Print: arXiv:1708.09408 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS
Abstract Service
Abstract and PDF from arXiv.org; Journal Server - JHEP
-
The Impact of Two-Loop Effects on the Scenario of MSSM Higgs Alignment without Decoupling
Howard E. Haber, Sven Heinemeyer, Tim Stefaniak. Aug 15, 2017. 31 pp.
IFT-UAM-CSIC-17-074, SCIPP-17/09
Published in Eur.Phys.J. C77 (2017) 742
DOI: 10.1140/epjc/s10052-017-5243-5
Published version: [PDF]
e-Print: arXiv:1708.04416 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract and PDF from arXiv.org; Journal Server - Eur.Phys.J.C.
-
High scale flavor alignment in two-Higgs doublet models and its phenomenology
Stefania Gori, Howard E. Haber, Edward Santos. Mar 16, 2017. 39 pp.
SCIPP-17/00
Published in JHEP 06 (2017) 110
DOI: 10.1007/JHEP06(2017)110
Published version: [PDF]
e-Print: arXiv:1703.05873 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract and Postscript and PDF from arXiv.org; Journal Server - JHEP
-
The Light and Heavy Higgs Interpretation of the MSSM
Philip Bechtle, Howard E. Haber, Sven Heinemeyer, Oscar Stål, Tim Stefaniak, Georg Weiglein, Lisa Zeune. Aug 1, 2016. 63 pp.
BONN-TH-2016-06, DESY-16-151, IFT-UAM-CSIC-16-068, NIKHEF-2016-033, SCIPP-16-10
Published in Eur.Phys.J. C77 (2017) 67
DOI: 10.1140/epjc/s10052-016-4584-9
Published version: [PDF]
e-Print: arXiv:1608.00638 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS
Abstract Service
Abstract and PDF from arXiv.org; Journal Server - Eur.Phys.J.C.
-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS
Abstract Service
Links to my 2016 publications:
-
Perturbation Theory in Supersymmetric QED: Infrared Divergences and Gauge Invariance
Michael Dine, Patrick Draper, Howard E. Haber, Laurel Stephenson Haskins. Jul 23, 2016. 28 pp.
SCIPP-16/08
Published in Phys.Rev. D94 (2016) 095003
DOI: 10.1103/PhysRevD.94.095003
Published version: [PDF]
e-Print: arXiv:1607.06995 [hep-th] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS
Abstract Service
Abstract and PDF from arXiv.org; Journal Server - Phys.Rev
-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS
Abstract Service
-
Partially Natural Two Higgs Doublet Models
Patrick Draper, Howard E. Haber, Joshua T. Ruderman. May 10, 2016. 31 pp.
SCIPP-16/06 and NSF-KITP-16-04
Published in JHEP 06 (2016) 124
DOI: 10.1007/JHEP06(2016)124
Published version: [PDF]
e-Print: arXiv:1605.03237 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS
Abstract Service
Abstract and PDF from arXiv.org; Journal Server - JHEP
-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS
Abstract Service
-
Scrutinizing the Alignment Limit in Two-Higgs-Doublet Models. Part 2: mH=127 GeV
Jérémy Bernon (LPSC, Grenoble), John F. Gunion (UC, Davis (main)), Howard E. Haber (UC, Santa Cruz, Inst. Part. Phys.), Yun Jiang (UC, Davis & Bohr Inst. & Copenhagen U.), Sabine Kraml (LPSC, Grenoble). Nov 11, 2015. 43 pp.
LPSC15274, UCD-2015-002, SCIPP-15/13
Published in Phys.Rev. D93 (2016) 035027
DOI: 10.1103/PhysRevD.93.035027
Published version: [PDF]
e-Print: arXiv:1511.03682 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract and PDF from arXiv.org; Journal Server - Phys.Rev
-
On the Alignment Limit of the NMSSM Higgs Sector
Marcela Carena, Howard E. Haber, Ian Low, Nausheen R. Shah, Carlos E. M. Wagner. Oct 30, 2015. 60 pp.
EFI-15-32, FERMILAB-PUB-15-407-T, MCTP-15-15, SCIPP 15/12, WSU-HEP-1505
Published in Phys.Rev. D93 (2016) 035013
DOI: 10.1103/PhysRevD.93.035013
Published version: [PDF]
e-Print: arXiv:1510.09137 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract and PDF from arXiv.org; Journal Server - Phys.Rev
Links to my 2015 publications:
-
New LHC Benchmarks for the CP-conserving Two-Higgs-Doublet Model
Howard E. Haber, Oscar Stål. July 15, 2015. 37 pp.
SCIPP-15-10
Published in Eur.Phys.J. C75 (2015) 491, Erratum-ibid. C76 (2016) 312
DOI: 10.1140/epjc/s10052-015-3697-x, 10.1140/epjc/s10052-016-4151-4
Published version: [PDF] [Erratum]
e-Print: arXiv:1507.04281 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract and PDF from arXiv.org; Journal Server - Eur.Phys.J.C.; Journal Server - Erratum-ibid.
-
Scrutinizing the Alignment Limit in Two-Higgs-Doublet Models. Part 1: mh = 125 GeV
Jérémy Bernon, John F. Gunion, Howard E. Haber, Yun Jiang, Sabine Kraml. July 3, 2015. 48 pp.
LPSC15154, UCD-2015-001, SCIPP-15/08
Published in Phys.Rev. D92 (2015) 075004
DOI: 10.1103/PhysRevD.92.075004
Published version: [PDF]
e-Print: arXiv:1507.00933 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract and PDF from arXiv.org; Journal Server - Phys.Rev
-
Preserving the validity of the Two-Higgs Doublet Model up to the Planck scale
Pedro Ferreira (Lisbon, ISEL & Lisbon U., CFTC), Howard E. Haber, Edward Santos (UC, Santa Cruz). May 15, 2015. 36 pp.
SCIPP-15-07
Published in Phys.Rev. D92 (2015) 033003, Erratum-ibid. D94 (2016) 059903
DOI: 10.1103/PhysRevD.92.033003, 10.1103/PhysRevD.94.059903
Published version: [PDF] [Erratum]
e-Print: arXiv:1505.04001 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract and Postscript and PDF from arXiv.org; Journal Server - Phys.Rev.; Journal Server - Erratum-ibid.
-
Complementarity Between Non-Standard Higgs Boson Searches and Precision Higgs Boson Measurements in the MSSM
Marcela Carena, Howard E. Haber, Ian Low, Nausheen R. Shah, Carlos E. M. Wagner. Oct 18, 2014. 43 pp.
EFI-14-36, FERMILAB-PUB-14-392-T, MCTP-14-37, SCIPP-14-16
Published in Phys.Rev. D91 (2015) 035003
DOI: 10.1103/PhysRevD.91.035003
Published version: [PDF]
e-Print: arXiv:1410.4969 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
|
ADS
Abstract Service
Abstract and Postscript and PDF from arXiv.org; Journal Server - Phys.Rev.
Twelve selected publications published from 2005--2014 are listed below.
-
Probing wrong-sign Yukawa couplings at the LHC and a future linear collider
P.M. Ferreira, John F. Gunion, Howard E. Haber, Rui Santos. Mar 19, 2014. 24 pp.
SCIPP-14-02, UCD-2014-2
Published in Phys.Rev. D89 (2014) 115003
DOI: 10.1103/PhysRevD.89.115003
Published version: [PDF]
e-Print: arXiv:1403.4736 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
ADS Abstract Service
Abstract and Postscript and PDF from arXiv.org; Journal Server - Phys.Rev.
-
Decoupling of the Right-handed Neutrino Contribution to the Higgs Mass in Supersymmetric Models
Patrick Draper, Howard E. Haber. Apr 22, 2013. 27 pp.
SCIPP-13-04.
Published in Eur.Phys.J. C73 (2013) 2522
DOI: 10.1140/epjc/s10052-013-2522-7
Published version: [PDF]
e-Print: arXiv:1304.6103 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS
Abstract Service
Abstract and PDF from arXiv.org; Journal Server - Eur.Phys.J.C.
-
Mass-degenerate Higgs bosons at 125 GeV in the Two-Higgs-Doublet Model.
P.M. Ferreira, Howard E. Haber, Rui Santos, Joao P. Silva. Nov 2012. 17 pp.
SCIPP-12-14.
Published in Phys.Rev. D87 (2013) 055009
DOI: 10.1103/PhysRevD.87.055009
Published version: [PDF]
e-Print: arXiv:1211.3131 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract and Postscript and PDF from arXiv.org; Journal Server - Phys.Rev.
-
Group-theoretic Condition for Spontaneous CP Violation.
Howard E. Haber (UC, Santa Cruz), Ze'ev Surujon (UC, Irvine). Jan 2012. 25 pp.
SCIPP-12-01, UCI-TR-2012-01.
Published in Phys.Rev. D86 (2012) 075007
DOI: 10.1103/PhysRevD.86.075007
Published version: [PDF]
e-Print: arXiv:1201.1730 [hep-ph] PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS
Abstract Service
Abstract and Postscript and PDF from arXiv.org; Journal Server - Phys.Rev.
-
Basis-independent methods for the two-Higgs-doublet model III: The CP-conserving limit, custodial symmetry, and the oblique parameters S, T, U.
Howard E. Haber, Deva O'Neil (UC, Santa Cruz). Nov 2010. 58 pp.
SCIPP-10-18.
Published in Phys.Rev. D83 (2011) 055017
DOI: 10.1103/PhysRevD.83.055017
Published version: [PDF]
e-Print: arXiv:1011.6188 [hep-ph]-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
Abstract and Postscript and PDF from arXiv.org; Journal Server - Phys.Rev.
Supersymmetric Monojets at the Large Hadron Collider.
Benjamin C. Allanach (Cambridge U., DAMTP), Sebastian Grab, Howard E. Haber (UC, Santa Cruz). Oct 2010. 42 pp.
DAMTP-2010-83, SCIPP-10-16.
Published in JHEP 01 (2011) 138, Erratum-ibid. 07 (2011) 087, Erratum-ibid. 09 (2011) 027
DOI: 10.1007/JHEP01(2011)138, 10.1007/JHEP07(2011)087, 10.1007/JHEP09(2011)027
Published version: [PDF] [Erratum 1] [Erratum 2]
e-Print: arXiv:1010.4261 [hep-ph]-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
Abstract and Postscript and PDF from arXiv.org; Journal Server - JHEP; Journal Server - Erratum-ibid.; Journal Server - Erratum-ibid.
Generalized CP symmetries and special regions of parameter space in the two-Higgs-doublet model
P.M. Ferreira (Lisbon, ISEL & Lisbon, IST), Howard E. Haber (UC, Santa Cruz), Joao P. Silva (Lisbon, ISEL & Lisbon, IST). Feb 2009. 20 pp.
Published in Phys.Rev. D79 (2009) 116004
DOI: 10.1103/PhysRevD.79.116004
Published version: [PDF]
e-Print: arXiv:0902.1537 [hep-ph] | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract and PDF from arXiv.org; Journal Server - Phys.Rev
-
Hard supersymmetry-breaking 'wrong-Higgs' couplings of the MSSM.
Howard E. Haber, John D. Mason (UC, Santa Cruz). Nov 2007. 32 pp.
SCIPP-07-16.
Published in Phys.Rev. D77 (2008) 115011
DOI: 10.1103/PhysRevD.77.115011
Published version: [PDF]
e-Print: arXiv:0711.2890 [hep-ph]-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
Abstract and Postscript and PDF from arXiv.org; Journal Server - Phys.Rev.
Seesaw mechanism in the sneutrino sector and its consequences.
Athanasios Dedes (Durham U., IPPP & Ioannina U.), Howard E. Haber (UC, Santa Cruz), Janusz Rosiek (Durham U., IPPP & Warsaw, CFT). Jul 2007. 63 pp.
IPPP-07-16,CPT-07-32, SCIPP-07-10.
Published in JHEP 11 (2007) 059
DOI: 10.1088/1126-6708/2007/11/059
Published version: [PDF]
e-Print: arXiv:0707.3718 [hep-ph]-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
Abstract and Postscript and PDF from arXiv.org; Journal Server - JHEP; JHEP Electronic Journal Server
Basis-independent methods for the two-Higgs-doublet model. II. The Significance of tan beta.
Howard E. Haber, Deva O'Neil (UC, Santa Cruz, Inst. Part. Phys.). Feb 2006. 48 pp.
SCIPP-06-01.
Published in Phys.Rev. D74 (2006) 015018, Erratum-ibid. D74 (2006) 059905
DOI: 10.1103/PhysRevD.74.015018, 10.1103/PhysRevD.74.059905
Published version: [PDF] [Erratum]
e-Print: hep-ph/0602242 | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract and Postscript and PDF from arXiv.org; Journal Server - Phys.Rev.
Conditions for CP-violation in the general two-Higgs-doublet model
John F. Gunion (UC, Davis (main)), Howard E. Haber (UC, Santa Cruz, Inst. Part. Phys.). Jun 2005. 46 pp.
Published in Phys.Rev. D72 (2005) 095002
SCIPP-04-16, UCD-2004-29
DOI: 10.1103/PhysRevD.72.095002
Published version: [PDF]
e-Print: hep-ph/0506227 | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS
Abstract Service
Abstract and Postscript and PDF from arXiv.org; Journal Server - Phys.Rev. -
Basis-independent methods for the two-Higgs-doublet model
Sacha Davidson (Durham U., IPPP & Lyon, IPN), Howard E. Haber (Durham U., IPPP & UC, Santa Cruz). Apr 2005. 45 pp.
IPPP-03-23, DCPT-03-46, SCIPP-04-15.
Published in Phys.Rev. D72 (2005) 035004, Erratum-ibid. D72 (2005) 099902
DOI: 10.1103/PhysRevD.72.035004, 10.1103/PhysRevD.72.099902
Published version: [PDF] [Erratum]
e-Print: hep-ph/0504050 | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract and Postscript and PDF from arXiv.org; Phys. Rev. D Server
My three most highly cited papers (not including reviews) are listed below.
-
Can the mass of the lightest Higgs boson of the minimal supersymmetric model be larger than m(Z)?
Howard E. Haber, Ralf Hempfling (UC, Santa Cruz). Nov 1990. 12 pp.
Published in Phys.Rev.Lett. 66 (1991) 1815-1818
SCIPP-90-42
DOI: 10.1103/PhysRevLett.66.1815
Published version: [PDF]
-
Higgs Bosons in Supersymmetric Models. 1.
J.F. Gunion (UC, Davis), Howard E. Haber (UC, Santa Cruz & SLAC). Aug 1984. 111 pp.
Published in Nucl.Phys. B272 (1986) 1, Erratum-ibid. B402 (1993) 567-569
SLAC-PUB-3404.
DOI: 10.1016/0550-3213(86)90340-8; 10.1016/0550-3213(93)90653-7
Published version: [PDF] [Erratum]
-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
CERN Library Record ; SLAC Document Server; Journal Server - Nuclear Physics B; . Journal Server - Erratum-ibid.
-
The CP conserving two Higgs doublet model: The Approach to the decoupling limit
John F. Gunion (UC, Davis), Howard E. Haber (UC, Santa Cruz). Jul 2002. 42 pp.
SCIPP-02-10.
Published in Phys.Rev. D67 (2003) 075019
DOI: 10.1103/PhysRevD.67.075019
Published version: [PDF]
e-Print: hep-ph/0207010 | PDF-
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract and Postscript and PDF from arXiv.org; Phys. Rev. D Server
Webpage for
Two-component spinor techniques and Feynman rules for
quantum field theory and supersymmetry, maintained by Stephen
P. Martin.
Both the arXiv version and the Physics Reports version
use the spacetime metric signature (+1,-1,-1,-1),
as is found for example in the field theory textbooks by
Ramond, and by
Peskin and Schroeder
.
However, many people including
one of the authors (S.P. Martin) prefer the metric signature
(-1, +1, +1, +1),
as is
found for example in the textbooks by
Weinberg, by
Wess and Bagger,
by
Srednicki, and
in Martin's
Supersymmetry Primer.
Here is a PDF file of v6 of our review with the (-1, +1, +1, +1) metric
convention, which should be identical in content in every other
respect:
DHMspinors_v6.pdf.
Both the (+1,-1,-1,-1) and the (-1, +1, +1, +1) metric versions were made
from the same source files available from the arXiv.
The choice of metric signature is implemented by simply changing
a single character in the main LaTeX source file, namely the
argument
of line 20, with \def\signofmetric{0} corresponding
to the (+1,-1,-1,-1) metric and \def\signofmetric{1} to the
(-1, +1, +1, +1) metric. Note that the pdf file is produced with pdflatex.
The list of known corrections to the Physics Reports version as of May 2022
is here:
DHM_corr_PhysicsReports.pdf.
These corrections have all been implemented (along with some
additional enhancements) and can be found in
version
6 of arXiv:0812.1594 (313 pages, May 2022).
Any subsequent corrections to version
6 of arXiv:0812.1594 will be posted on
https://www.niu.edu/spmartin/spinors/.
Links to Conference proceedings, 2013--2022:
Howard E. Haber.
May 17, 2022. 15 pp.
Invited talk at DISCRETE 2020-2021: 7th Symposium on Prospects in the Physics of Discrete Symmetries, November 29--December 3, 2021
Published in PoS(DISCRETE2020-2021)010
Published version: [PDF]
e-Print: arXiv:2205.07578 [hep-ph] | PDF
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract and
PDF from
arXiv.org
Howard E. Haber.
May 15, 2018. 4 pp.
SCIPP 18/03.
Contribution to the Proceedings of the 53th Rencontres de Moriond, QCD Session, 17--24 March 2018
e-Print: arXiv:1805.05754 [hep-ph] | PDF
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS
Abstract Service
Abstract and
PDF from
arXiv.org
Howard E. Haber.
Jan 8, 2017. 12 pp.
Invited talk at Charged 2016: Prospects for Charged Higgs Discovery at Colliders, 3--6 October 2016
Published in PoS(CHARGED2016)029
Published version: [PDF]
e-Print: arXiv:1701.01922 [hep-ph] | PDF
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract and
Postscript
and PDF from
arXiv.org;
INSPIRE HEP Conference database listing
[Conference
C16-10-03.1 | Contributions];
Journal Server -
Proceedings of Science
Howard E. Haber.
Dec 31, 2013. 15 pp.
SCIPP-13-15.
Published in the Proceedings of the Toyama International
Workshop on Higgs as a Probe of New Physics 2013 (HPNP2013) on eConf
e-Print: arXiv:1401.0152 [hep-ph] | PDF
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract and
Postscript
and PDF from
arXiv.org;
INSPIRE HEP Conference database listing
[Conference
C13-02-13.1 | Contributions]
Articles on the Higgs boson meant for a broader audience can be
found below.
Howard E. Haber (UC, Santa Cruz).
Oct 4, 2022. 8 pp.
Published in the September 2022 issue of the CERN EP
Newsletter of the EP department
URL: https://ep-news.web.cern.ch/content/higgs-boson-physics-view-ahead
Howard E. Haber (UC, Santa Cruz).
Sept 2018.
Published in Physics 11 (2018) 91
DOI: 10.1103/Physics.11.91
Published version:
[PDF]
Howard E. Haber (UC, Santa Cruz).
Mar 2012.
Published in Physics 5 (2012) 32
DOI: 10.1103/Physics.5.32
Published version:
[PDF]
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
Journal Server - Physics
Howard E. Haber (UC, Santa Cruz).
Aug. 2006.
Published in
Symmetry Magazine, volume 3, issue 6 (August, 2006)
URL:
https://www.symmetrymagazine.org/article/august-2006/60-seconds-higgs-boson
Published version:
[PDF]
III. Published Reviews
Benjamin
C. Allanach (Cambridge
U., DAMTP), Howard
E. Haber (UC, Santa Cruz).
Aug. 2023. 53 pp.
PDF
from the 2024 edition of the Review of Particle Physics
Particle
Data Group Collaboration (S. Navas et al.). August
2024. 2382 pp.
Published in Phys. Rev. D 110, 030001 (2024)
DOI: doi.org/10.1103/PhysRevD.110.030001
Published version:
[PDF]
Particle Data Group (PDG) webpage: [HTML]
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
Link
to Fulltext
P. Slavich,
S. Heinemeyer,
E. Bagnaschi,
H. Bahl,
M. Goodsell,
H.E. Haber,
et al.
Dec 31, 2020. 83 pp.
DESY 20-229, DESY-20-229, IFT-UAM/CSIC-20-184, FR-PHENO-2020-021, KA-TP-23-2020,
MPP-2020-235, KA-TP-23-2020, MPP-2020-235, P3H-20-086, TTK-20-53
Published in Eur.Phys.J. C81 (2021) 450
DOI: 10.1140/epjc/s10052-021-09198-2
Published version: [PDF]
e-Print: arXiv:2012.15629 [hep-ph] | PDF
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
CERN Document Server; ADS Abstract Service; Link to Article from SCOAP3
Abstract and
PDF from
arXiv.org
Howard E. Haber, Laurel Stephenson Haskins.
Dec 16, 2017. 144 pp.
SCIPP-17-11
Conference: C16-06-06.15,
pp. 355--499
Proceedings
Published in
Chapter 6 of TASI 2016: Anticipating
the Next Discoveries in Particle Physics, edited by Rouven Essig
and Ian Low (World Scientific, Singapore, 2018).
DOI: 10.1142/9789813233348_0006
e-Print: arXiv:1712.05926 [hep-ph] | PDF
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract and
PDF from
arXiv.org
D.M. Asner, T. Barklow, C. Calancha, K. Fujii, N. Graf, H.E. Haber, A. Ishikawa, S. Kanemura, S. Kawada, M. Kurata et al..
Oct 23, 2013. 152 pp.
e-Print: arXiv:1310.0763 [hep-ph] | PDF
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
| ADS Abstract Service
Abstract
and PDF from
arXiv.org
P.M. Ferreira (Lisbon, ISEL & Lisbon, IST), Howard E. Haber (UC, Santa Cruz),
M. Maniatis
(Heidelberg
U.),
O. Nachtmann
(Heidelberg
U.), Joao P. Silva (Lisbon, ISEL & Lisbon, IST).
Oct 2010. 31 pp.
SCIPP-10-15, HD-THEP-10-1.
Published in Int.J.Mod.Phys. A26 (2011) 769-808
DOI: 10.1142/S0217751X11051494
Published version:
[PDF]
e-Print: arXiv:1010.0935 [hep-ph]
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
Abstract and
Postscript
and PDF from arXiv.org; Journal Server - Int.J.Mod.Phys.
Herbi K. Dreiner,
Howard E. Haber,
Stephen P. Martin.
Dec 2008. 246 pp.
BN-TH-2008-12, SCIPP-08-08.
Published in Phys.Rept. 494 (2010) 1-196
DOI: 10.1016/j.physrep.2010.05.002
Published version:
[PDF]
Corrected version of the published review with a few
enhancements, with the mostly minus metric
[PDF]
Corrected version of the published review with a few
enhancements, with the mostly plus metric
[PDF]
e-Print: arXiv:0812.1594 [hep-ph]
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
Abstract and
Postscript
and PDF from arXiv.org; Journal Server - Phys.Rept.
Marcela Carena (Fermilab), Howard E. Haber (UC, Santa Cruz).
Aug 2002. 87 pp.
hep-ph/0208209,FERMILAB-PUB-02-114-T, SCIPP-02-07.
Published in Prog.Part.Nucl.Phys. 50 (2003) 63-152
DOI: 10.1016/S0146-6410(02)00177-1
Published version:
[PDF]
e-Print: hep-ph/0208209
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
Abstract and
Postscript
and PDF from arXiv.org; Journal Server - Prog.Part.Nucl.Phys.; ADS Abstract Service; CERN Library Record ; Fermilab Library Server (fulltext available); Science Direct; WORLDSCI
Howard E. Haber (UC, Santa Cruz & Santa Barbara, KITP).
Apr 1994. 83 pp.
hep-ph/9405376, SCIPP-93-49, NSF-ITP-94-30, C93-07-26.
Published in Stanford 1993, Spin structure in high energy
processes, pp. 231-272
Presented at Conference: C93-07-26
e-Print: hep-ph/9405376
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
Abstract from arXiv.org; KEK scanned document ; CERN Library Record
Howard E. Haber (UC, Santa Cruz).
Mar 1991. 136 pp.
SCIPP-91-06
Invited lectures given at Conference: C90-06-03 (Boulder TASI 90:340-475), p.340-475
Howard E. Haber (UC, Santa Cruz & SLAC), Gordon L. Kane (Michigan U.).
Jan 1984. 376 pp.
UM-HE-TH-83-17, SCIPP-85-47.
Published in Phys.Rept. 117 (1985) 75-263
DOI: 10.1016/0370-1573(85)90051-1
Published version:
[PDF]
[Erratum]
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
Journal Server - Phys.Rept.; KEK scanned document
IV. Published Books
Co-authored books
Herbi K. Dreiner,
Howard E. Haber,
Stephen P. Martin.
Jun 2023. 1009 pp.
Links to From Spinors to Supersymmetry at the Cambridge
University Press webpage:
[Overview
| Hardback
|
eBook]
Link to
Resources
and Errata
The book can also be purchased from Amazon via the following
link.
John F. Gunion (UC, Davis), Howard E. Haber (UC, Santa Cruz), Gordon L. Kane (Michigan U.), Sally Dawson (Brookhaven).
Jun 1989. 404 pp.
SCIPP-89/13, UCD-89-4, BNL-41644.
Published in Front. Phys. 80 (2000) 1-448
Link to The Higgs Hunter's Guide at the
Perseus
Books webpage. See also the
Routledge (member of Taylor &
Francis Group) webpage.
John F. Gunion (UC, Davis), Howard E. Haber (UC, Santa Cruz), Gordon L. Kane (Michigan U.), Sally Dawson (Brookhaven).
Dec 1992. 5 pp.
hep-ph/9302272, SCIPP-92-58.
e-Print: hep-ph/9302272
References
| BibTeX
| LaTeX(US)
| LaTeX(EU)
| Harvmac
| EndNote
Abstract and
Postscript
and PDF from arXiv.org
Edited books
H.E. Haber, (ed.) (UC, Santa Cruz), A.E. Nelson, (ed.) (Washington U., Seattle).
2004. 892 pp.
ISBN-9789812388926.
Prepared for Conference: C02-06-02.1 (River Edge, USA: World Scientific (2004) 892 p)
Link to
Particle Physics
and Cosmology webpage at World Scientific Publishing.
T.L. Barklow, (ed.) (SLAC), S. Dawson, (ed.) (Brookhaven), H.E. Haber, (ed.) (UC, Santa Cruz), J.L. Siegrist, (ed.) (LBL, Berkeley).
1996.
Published in Singapore, Singapore: World Scientific (1996) 736 p. (Advanced series on directions in high energy physics. 16)
Link to
Electroweak Symmetry
Breaking and New Physics at the TeV Scale webpage at World Scientific Publishing.
H.E. Haber, (Ed.).
1987.
Published in SINGAPORE, SINGAPORE: WORLD SCIENTIFIC (1987) 497-953
Link to
From the Planck Scale to the Weak Scale: Toward a Theory of the Universe webpage at World Scientific Publishing.
H.E. Haber, (Ed.).
1987.
Published in SINGAPORE, SINGAPORE: WORLD SCIENTIFIC (1987) 1-495
Link to
From the Planck Scale to the Weak Scale: Toward a Theory of the Universe webpage at World Scientific Publishing.
V. Teaching
- Winter, 2025 Physics 205 Introduction to Research "Research on the Theory of the Terascale" [PDF | Powerpoint]
- Winter, 2024 Physics 214 Electromagnetism II
- Spring, 2023 Physics 251 Group Theory and Modern Physics
- Spring, 2020 Physics 222 Quantum Field Theory III
- Fall, 2019 Physics 116A Mathematical Methods in Physics I
- Winter, 2018 Physics 215 Introduction to Non-Relativistic Quantum Mechanics
- Fall 2016 Physics 217 Quantum Field Theory I
- Winter 2016 Physics 218 Quantum Field Theory II
- Fall, 2015 Physics 171 General Relativity, Black Holes, and Cosmology
- Fall, 2012 Physics 116C Mathematical Methods in Physics III
- Spring, 2012 Physics 216 Advanced Topics in Non-Relativistic Quantum Mechanics
- Fall, 2009 Physics 139B Quantum Mechanics II
- Winter, 2009 Physics 5B Introduction to Physics II
- Winter, 2000 Physics 112 Thermodynamics and Statistical Mechanics
VI. Notes and other writings
- The Hamiltonian of a free Majorana fermion field [PDF | PS]
- Acceleration and Force in Special Relativity [PDF | PS]
- Thomas Precession and the BMT equation [PDF | PS]
- The tensor spherical harmonics [PDF | PS]
- Evaluating integrals arising from Barr-Zee diagrams [PDF | PS]
- Exponentiating the Lie algebra of the Lorentz group [PDF | PS]
- Rational approximations to ln 2 short version: [PDF | PS]; long version: [PDF | PS]
- Generalized Functions for Physics [PDF | PS]
- Evaluating the finite part of the Passarino-Veltman function B0(p2;m12,m22) [PDF | PS]
- Evaluating the one-loop function arising in h→γγ [PDF | PS]
- Analytic formulae for the Feynman propagator in coordinate space [PDF | PS]
- A Tale of Three Diagonalizations [PDF | PS]
- Notes on the Matrix Exponential and Logarithm [PDF | PS]
- The characteristic polynomial [PDF | PS]
- What is the group of conjugate symplectic matrices? [PDF | PS]
- Parameterization of real orthogonal antisymmetric matrices [PDF | PS]
- Toward a set of 2HDM benchmarks [PDF | PS]
- The eigenvalues of the quadratic Casimir operator and second-order indices of a simple Lie algebra [PDF | PS]
- Notes on basis changes and matrix diagonalization [PDF | PS]
- Notes on the complex inverse trigonometric and hyperbolic functions and their principal values [PDF | PS]
- Electron wave function and mass renormalization in QED [PDF | PS]
- Proof of a trace inequality in matrix algebra [PDF | PS]
- Notes on the spontaneous breaking of SU(N) and SO(N) via a second-rank tensor multiplet [PDF | PS]
- Notes on antisymmetric matrices and the pfaffian [PDF | PS]
- Complex representation of scalar fields and the embedding of U(n) in SO(2n) [PDF | PS]
- The probability that a product of random numbers is less than a fixed constant [PDF | PS]
- Massless Majorana and Weyl fermions cannot be distinguished [PDF | PS]
VII. Talks at conferences, workshops and schools, 2004--2025
2025 Conferences and workshops
- Corfu2025 Workshop on Future Accelerators, at the Corfu Summer School and Workshops on Elementary Particle Physics and Gravity, in Mon-Repos, Corfu, Greece, May 1, 2025 Higgs physics at future e+e- colliders [PDF]
- The 7th International Workshop on "Higgs as a Probe of New Physics" (HPNP2025), at Osaka University, in Osaka, Japan, June 10, 2025 RG-stable parameter relations of a scalar field theory in absence of a symmetry [PDF]
2024 Conferences and workshops
- Cosmology, Astrophysics, Theory and Collider Higgs 2024 (CATCH22+2), at the Dublin Institute for Advanced Study (DIAS), in Dublin, Ireland, May 1, 2024 Classes of complete dark photon models constrained by Z Physics [PDF]
- PLANCK 2024: 26th International Conference from the Planck Scale to the Electroweak Scale, In Lisbon, Portugal, June 5, 2024 Flavor-nondiagonal neutral Higgs Yukawa couplings revisited [PDF]
- 31st International Conference on Supersymmetry and Unification of Fundamental Interactions: Theory meets Experiment (SUSY 2024), in Madrid, Spain, June 10, 2024 Classes of complete dark photon models constrained by Z Physics [PDF]
- 2024 Workshop on Multi-Higgs Models, at the Instituto Superior Técnico in Lisbon, Portugal, September 3, 2024 Flavor-nondiagonal neutral Higgs Yukawa couplings revisited [PDF]
- Extended scalar sectors from all angles, at CERN in Geneva, Switzerland, October 25, 2024 Flavor-nondiagonal neutral Higgs Yukawa couplings revisited [PDF]
2023 Conferences and workshops
- "Herbi Fest"--Pursuing Physics Beyond the Standard Model: a symposium in honor of Herbi Dreiner on the occasion of his 60th birthday, at the Bethe Center for Theoretical Physics, University of Bonn, in Bonn, Germany, March 28, 2023 Adventures from spinors to SUSY [PDF]
- International Workshop on Future Linear Colliders (LCWS2023), at SLAC National Accelerator Laboratory in Menlo Park, CA USA, May 17, 2023 P-even, CP-violating Signals in Scalar-Mediated Processes [PDF]
- PLANCK 2023: 25th International Conference from the Planck Scale to the Electroweak Scale, at the University of Warsaw in Warsaw, Poland, May 22, 2023 Higgs Boson Physics—The View Ahead [PDF]
- Beyond the SM from Colliders to the Early Universe: a symposium in honor of Marcela Carena and Carlos Wagner on the occasion of their 60th birthdays, at the University of Chicago in Chicago, IL USA and at Fermilab in Batavia, IL USA, May 28, 2023 My Journey through Physics with Marcela and Carlos [PDF]
- The 6th International Workshop on "Higgs as a Probe of New Physics" (HPNP2023), at Osaka University, in Osaka, Japan, June 5, 2023 Signals of new heavy scalars in the flavor-aligned 2HDM [PDF]
- pre-SUSY school 2023, at the University of Southampton, in Southampton, England, July 13, 2023 Supersymmetry and Higgs Physics [PDF]
- The XXX International Conference on Supersymmetry and Unification of Fundamental Interactions (SUSY 2023), at the University of Southampton, in Southampton, England, July 21, 2023 Supersymmetry Confronts a SM-Like Higgs Boson [PDF]
- Higgs Days at Santander 2023, in Santander, Spain, September 6, 2023 Signals of new heavy scalars in the flavor-aligned 2HDM [PDF]
- Scalars 2023, at the University of Warsaw in Warsaw, Poland, September 13, 2023 Scalar revelations at future e+e- colliders [PDF]
2022 Conferences and workshops
- The XXIX International Conference on Supersymmetry and Unification of Fundamental Interactions (SUSY 2022), at the University of Ioannina in Ioannina, Greece, June 29, 2022 The anapole moment of a charged lepton in softly-broken Supersymmetric QED [PDF]
- Workshop on Multi-Higgs Models, at the Instituto Superior Técnico in Lisbon, Portugal, August 30, 2022 P-even, CP-violating Signals in Scalar-Mediated Processes [PDF]
- IDT-WG3-Phys Open Meeting, online via zoom, November 17, 2022 P-even, CP-violating Signals in Scalar-Mediated Processes [PDF]
2021 Conferences and workshops
- The 5th International Workshop on "Higgs as a Probe of New Physics Special Edition 2021" (HPNP2021), in Osaka, Japan (held online), March 27, 2021 Exceptional regions of the 2HDM parameter space [PDF]
- 49th SLAC Summer Institute (SSI 2021), at SLAC, Stanford, CA USA (held online), August 27, 2021 Higgs Boson Physics—The View Ahead [PDF]
- Charged Higgs Online Workshop, August 30, 2021 Extended Higgs sector at present and future colliders [PDF]
- DISCRETE 2020-2021, December 3, 2021 A natural mechanism for a SM-like Higgs boson in the 2HDM without decoupling [PDF]
 Professional talks
at conferences and workshops in previous years are stored
here.
Professional talks
at conferences and workshops in previous years are stored
here.
Schools and Pedagogical Lectures
- pre-SUSY school 2023, at the University of Southampton, in Southampton, England, July 13, 2023 Supersymmetry and Higgs Physics [PDF]
- 49th SLAC Summer Institute (SSI 2021), at SLAC, Stanford, CA USA (held online), August 27, 2021 Higgs Boson Physics—The View Ahead [PDF]
- Sorak Symposium reminiscence on Particle Physics, at NakSan Beach Hotel in Yang Yang, South Korea, August 15, 2019 The incomplete and biased history of the Higgsboson [PDF]
- Sorak Symposium reminiscence on Particle Physics, at NakSan Beach Hotel in Yang Yang, South Korea, August 15, 2019 Quo Vadis Higgs (or what the current Higgs data is trying to tell us) [PDF]
- The 46th SLAC Summer Institute--Standard Model at 50: Successes and Challenges
VIII. 2025 Conferences and workshops in particle physics
9th International Conference on High Energy Particle and Nuclear Physics in the LHC Era (HEPNP2025), January 6--10, 2025 at the Universidad Técnica Federico Santa María (UTFSM) in Valparaíso, Chile.
Linear Collider Vision Community Event 2025, January 8--10, 2025 at CERN in Geneva, Switzerland
DPF/DPB Forum on US contributions to the European Strategy Update, February 27, 2025, held online
The Aspen Winter Conference: Empowering the New Vision in High Energy Physics, March 2--7, 2025 at the Aspen Center for Physics in Aspen, CO USA
Joint March Meeting and April Meeting: APS Global Physics Summit, March 16--21, 2025 in Anaheim, CA USA
59th Rencontres de Moriond--Electroweak Interactions & Unified Theories, March 23--30, 2025 in La Thuile, Italy
The XXXII International Workshop on Deep Inelastic Scattering and Related Subjects (DIS2025), March 24--28, 2025 in Cape Town, South Africa
59th Rencontres de Moriond--QCD & High Energy Interactions, March 30--April 6, 2025 in La Thuile, Italy
Bay Area Particle Theory Seminar (BAPTS), April 4, 2025 at San Francisco State University (SFSU) in San Francisco, CA USA
The 14th KUTS meeting: "Precision SUSY Higgs Mass Calculation Initiative" (KUTS14), April 7--9, 2025 at the University of Freiburg in Freiburg, Germany
3rd Annual US Higgs Factory--Future Circular Collider (HF-FCC) Workshop, April 14--17, 2025, hosted jointly by Fermilab and Argonne National Laboratory
Corfu2025 Workshop on Future Accelerators, April 27--May 4, 2025 at the Corfu Summer School and Workshops on Elementary Particle Physics and Gravity, in Mon-Repos, Corfu, Greece
The 5th European
Consortium for Astroparticle Theory (EuCAPT) Symposium, May 5--7,
2025, online
The 13th Annual
Large Hadron Collider Physics Conference (LHCP2025), May 5--9,
2025 in Taipei, Taiwan
Higgs Pairs Workshop 2025, May 11--17, 2025 at the Hotel Hermitage, La Biodola, Isola d'Elba
Frontiers Beyond the
Standard Model, May 15--17, 2025 at the William I. Fine
Theoretical Physics Institute (FTPI) at the University of Minnesota in
Minneapolis, MN USA
Phenomenology 2025 Symposium (PHENO 2025), May 19--21,
2025 at the University of Pittsburgh and Carnegie Mellon University
in Pittsburgh, PA USA
FCC Week 2025, May
19--23, 2025 at the Vienna Imperial Palace (Wiener Hofburg) in Vienna, Austria
LoopFest XXIII,
May 21--23, 2025 at the University of Alberta in Edmonton, Alberta Canada
Bootstrap,
Holography & Swampland: Imprint of UV principles on IR physics,
May 25--June 15, 2025 at
the Aspen Center for Physics in Aspen, CO USA
PLANCK 2025: 27th International Conference from the Planck Scale to the
Electroweak Scale, May 26--30, 2025 in Padua, Italy
Fifteenth workshop of
the Long-Lived Particle Community (LLP2025), June 2--6, 2025 at
the Instituto de Física Corpuscular (IFIC) in València, Spain.
Navigating
new horizons: defining the next era of particle physics, June
2--27, 2025 at the Munich Institute for Astro-, Particle and
BioPhysics (MIAPbP) in Garching, Germany
Theoretical
Advanced Study Institute in ELementary Particle Physics (TASI
2025)--Threads in a Theory Tapestry, June 2--27, 2025 at the University of Colorado in Boulder,
CO USA
15th
Conference on the Intersections of Particle and Nuclear Physics
(CIPANP 2025), June 8--14, 2025 in Madison, Wisconsin USA
The
7th International Workshop on "Higgs as a Probe of New Physics"
(HPNP2025), June 9--13, 2025 at Osaka
University, in Osaka, Japan
Q+A for the National
Academies Report on Elementary Particle Physics, June 12, 2025 at
Fermilab in Batavia, IL USA
Collider Physics at the LHC and Beyond,
June 15--July 13, 2025 at
the Aspen Center for Physics in Aspen, CO USA
The strong CP problem
and its possible solutions, June 16--27, 2025 at the Pollica
Physics Centre, Castello dei Principi Capano, in Pollica (SA), Italy
Open Symposium
on the European Strategy for Particle Physics, June 23--27, 2025
at Lido di Venezia in Venice, Italy
XVII International
Conference on Interconnections between Particle Physics and Cosmology
(PPC 2025), June 23--28, 2025, hosted by The Institute of
Underground Science at SURF, at the Cadillac Jack's Resort in
Deadwood, South Dakota, USA
11th Workshop on Flavor
Symmetries and Consequences in Accelerators and Cosmology (FLASHY
2025), June 30--July 4, 2025 in Rome, Italy
19th edition of the Dark side
of the Universe (DSU) Workshop, July 7--11, 2025 in Montreal, Canada
Multi-Particle
Reactions from the Standard Model: spectroscopy, precision tests and
beyond, July 14--25, 2025, hosted jointly by UC Berkeley and
Lawrence Berkeley National Lab, in Berkeley, CA USA
Higgs Hunting
2025, July 15--17, 2025 at Orsay and Paris, France
XIV
International Conference on New Frontiers in Physics (ICNFP 2025),
July 17--31, 2025 at the Orthodox Academy of Crete (OAC), Kolymbari,
Crete, Greece
Workshop on
Multi-Particle Reactions from the Standard Model: spectroscopy,
precision tests and beyond, July 28--August 1, 2025 at Lawrence Berkeley National
Laboratory in Berkeley, CA USA
53rd SLAC
Summer Institute: Pathways to New Physics, July 28--August 8,
2025 (Zoom only),
at the Stanford Linear Accelerator Center in Menlo Park, CA USA
DPF Virtual Community
Meeting, July 31--August 1, 2025 via Zoom
2nd Annual U.S. Muon
Collider Community (USMCC) Meeting, August 7--8, 2025 at the
University of Chicago in Chicago, IL USA
Pre-SUSY School 2025, August 11--15, 2025 at the
University of California, Santa Cruz in Santa Cruz, CA USA
32nd International Conference on Supersymmetry and Unification of
Fundamental Interactions (SUSY 2025), August
18--23, 2025 at the
University of California, Santa Cruz in Santa Cruz, CA USA
Twentieth joint
CERN-Fermilab Hadron Collider Physics Summer School, August
19--28, 2025 at CERN in Geneva, Switzerland
Workshop on
the Standard Model and Beyond, August 24--September 3, 2025 at the
Corfu Summer School and Workshops on Elementary Particle Physics and Gravity, in Mon-Repos, Corfu, Greece
32nd International Symposium on Lepton Photon Interactions at High
Energies
(Lepton Photon 2025), August 25--29, 2025 in Madiscon, WI USA
Corfu2025 Workshop on
the Standard Model and Beyond, August 24--September 3, 2025 at the
Corfu Summer School and Workshops on Elementary Particle Physics and Gravity, in Mon-Repos, Corfu, Greece
32nd International Symposium on Lepton Photon Interactions at High
Energies
(Lepton Photon 2025), August 25--29, 2025 in Madiscon, WI USA
Opening Symposium: Max
Planck-IAS-NTU Center, September 1--3, 2025 at the
National Taiwan University (NTU) in Taipei, Taiwan.
The Invisibles
Workshop 2025, September 1--5, 2025 at CERN in Geneva, Switzerland
Higgs Days at
Santander 2025, September 8--12, 2025 in Santander, Spain
Scalars
2025, September 22--25, 2025 at the University of Warsaw in
Warsaw, Poland
HHH Workshop 2025,
September 29--October 1, 2025 at IUC Dubrovnik, Croatia
Bay Area Particle Theory Seminar (BAPTS),
October 3, 2025 at San Francisco State University (SFSU) in San
Francisco, CA USA
The 17th
International Symposium on Radiative Corrections: Applications of
Quantum Field Theory to Phenomenology (RADCOR 2025), October
5--10, 2025 at the Empires Hotel in Puri, Odisha, India
Beyond
Standard Model: From Theory to Experiment (BSM- 2025), October
6--9, 2025, in Istanbul, Turkey
Higgs@Capri 2025: First
Workshop on the Impact of Higgs Studies on New Theories of Fundamental
Interactions, October 6--10, 2025 at Villa Orlandi, Anacapri, Capri Island, Italy
2025
Annual Meeting of the Far West Section of the American Physical
Society, October 10--12, 2025 at the University of California,
Santa Cruz in Santa Cruz, CA USA
28th International
Conference on Particle Physics and Cosmology (COSMO-25), October
13--17, 2025 at Carnegie Mellon University in Pittsburgh, PA USA
44th International
Symposium on Physics in Collision (PIC-2025), October 20--23, 2025
at Zewail City of Science and Technology in Giza, Egypt
SEARCH Conference,
October 20--24, 2025 at CERN in Geneva, Switzerland
Linear Collider Workshop (LCWS 2025), October 20--24, 2025 in
Valencia, Spain
Higgs 2025,
October 27--31, 2025 at Brown University in Providence, RI USA
4th International
Symposium on the History of Particle Physics, November 10--13,
2025, at CERN in Geneva, Switzerland
Georg Fest, November 13, 2025 at DESY in Hamburg, Germany
The 22nd annual workshop
of the LHC Higgs Working Group, December 3--5, 2025, at CERN in
Geneva, Switzerland
US LHC Users Association annual meeting, December 16--18, 2025, at the
University of Washington in Seattle, WA USA
New
Directions in Theoretical Physics 5, January 6--9, 2026 at the
Higgs Centre for Theoretical Physics in Edunburgh, Scotland
The APS Global Physics Summit, March
15--20, 2026 in Denver, CO USA
The 15th KUTS meeting:
"Precision SUSY Higgs Mass Calculation Initiative"
(KUTS15), March 23--26, 2026
at the Karlsruhe Institute of Technology (KIT) in Karlsruhe, Germany
Precision
Lepton Physics: a window to new physics, April 7--30, 2026, at
the Munich Institute for Astro-, Particle and
BioPhysics (MIAPbP) in Garching, Germany
The 2026 APS Division of Particles and Fields (DPF) meeting, July
20--24, 2026 at Fermilab in Batavia, IL USA
Invisibles
26,
August 10--14, 2026 in Cantón Grande, 8, A Coruña, 15003, Spain
Higgs Hunting 2026, September 16--18, 2026 at Orsay and Paris, France
Higgs@GGI
2026, Spetember 28--October 23, 2026, at the Galileo Galilei
Institute in Arcetri, Florence, Italy
 Listings of conferences and
workshops from previous years are stored
here.
Listings of conferences and
workshops from previous years are stored
here.
IX. University Service
Faculty Perceptions of a UCSC Research Environment in Need of Restoration and Improvement, a report by Howard E. Haber and David M. Harrington, sponsored by the UCSC Committee on Research and contributed in May, 1998 to the Advisory Report of the Millennium Committee. [HTML]
University Committee on Research Policy (UCORP) 1995--1996 Public web page.
Should UC renew its contract with the Department of Energy (DOE) to manage the Lawrence Livermore National Laboratory and Los Alamos National Laboratory? The following web page documents the 1996 UC systemwide campus debate on this question. A town meeting was held on the UCSC campus on March 7, 1996 to discuss these issues.
X. Extracurricular Activities
Some of the physics students and I play softball in the UCSC intramural coed softball league. The fall season runs from early October to early December, and the spring season runs from early April to early June.
Our team, called Re-Entry, is sponsored by the STARS organization on campus, which provides support and counseling for returning (or re-entry) students to campus. You can follow our season exploits on the Re-Entry Team Webpage.
XI. Physics, Math and Computer Links
Book Price comparisons
CERN links
LHC Performance and Statistics
LHC Programme Coordination web pages
ATLAS Online Luminosity [for more details click here]
CMS Online Luminosity [for more details click here]
CERN Physics results
ATLAS Experiment--Public results
ATLAS Supersymmetry Physics results
CMS Supersymmetry Physics results
Electroweak and Higgs precision observables
LHC Higgs Cross Section Working Group (HXSWG)
SFitter Higgs coupling analysis
Higgs boson links
Precision SUSY Higgs Mass Calculation Initiative
SM Higgs production cross sections at √s = 13 TeV
SM Higgs Branching Ratios and Total Decay Widths
LHC Higgs Cross Section Working Group Twiki
Heavy Higgs and Beyond Standard Model subgroup of the HXSWG
Handbook of LHC Higgs Cross Sections: 1. Inclusive Observables [Postscript | PDF]
Handbook of LHC Higgs Cross Sections: 2. Differential Distributions [Postscript | PDF]
Handbook of LHC Higgs Cross Sections: 3. Higgs Properties [Postscript | PDF]
Handbook of LHC Higgs Cross Sections: 4. Deciphering the nature of the Higgs sector [PDF]
High Energy Physics links
High Energy Physics Software and Collider Tools
International Linear Collider
American Linear Collider Working Group
International Linear Collider (ILC) homepage
CLIC detector and physics study (CLICdp)--WG Physics Potential
Compact Linear Collider (CLIC)
Journals
Journal of Mathematical Physics
Physical Review Online Archive (PROLA)
Mathematics links
Mathematical Association of America
Meetings and Conferences organized by SCIPP Theory
Howie-Fest-70, February 7, 2022 at the University of California, Santa Cruz, CA USA (held online)
SCIPP Reunion Theory Symposium, April 24, 2015 at the University of California, Santa Cruz
The search for Fundamental Physics: Higgs Bosons & Supersymmetry, A symposium in honor of Michael Dine and Howard Haber on the occasion of their 60th Birthdays, January 4--6, 2013
West Coast LHC Theory meeting, May 21, 2010
Confronting Challenges in Theoretical Physics, A Symposium in Honor of Tom Banks and Willy Fischler on the Occasion of their 60th Birthdays June 15--16, 2009
RADCOR 2000, 5th International Symposium on Radiative Corrections, September 11--15, 2000
Particle physics outreach
Physikshow at the University of Bonn
Particle physics jobs
Theoretical Particle Physics Jobs Rumor Mill
High Energy Physics Postdoc Rumor Mill
Physics blogs
AsymptotiaPhysics links
Division of Particles and fields of the APS
Professional publishers
Search links
Snowmass 2021 links
The Particle Physics Community Planning Exercise
Tevatron physics results
Tevatron New Phenomena & Higgs Working Group
TeX and LaTeX links
Selected extracts from the Comprehensive LaTeX Symbol List [HTML | [PDF]
Using Imported Graphics in LaTeX and pdfLaTeX [PDF]
XII. Miscellaneous links of interest
Humor
Piled Higher and Deeper (Ph.D. Comics)
Sports
ESPN
National Basketball Association
San
Francisco Giants
Photographs that I have taken at various physics conferences and workshops can
be found at
this link.
Pictures of the Re-Entry coed softball team can be found
here.
Weather
XIII. Photographs
Last Updated: September 15, 2025



 Excerpted from a 1996 Foxtrot cartoon by Bill Amend.
A solution to this problem (along with the complete Foxtrot cartoon)
can be found
Excerpted from a 1996 Foxtrot cartoon by Bill Amend.
A solution to this problem (along with the complete Foxtrot cartoon)
can be found